Question Number 136680 by aupo14 last updated on 24/Mar/21

Answered by Olaf last updated on 24/Mar/21
![F(x) = ∫(dx/((x^2 +9)^2 )) Let x = 3shu F(u) = ∫((3chu)/((9sh^2 +9)^2 )) du F(u) = (1/(27))∫((chu)/(ch^4 u)) du F(u) = (1/(27))∫(du/(ch^3 u)) F(u) = (1/(27))∫((ch^2 u−sh^2 u)/(ch^3 u)) du F(u) = (1/(27))∫((1/(chu))−shu((shu)/(ch^3 u))) du F(u) = (1/(27))[2arctan(e^u )+shu(1/(2ch^2 u)) +∫chu(−(1/(2ch^2 u)))du F(u) = (1/(27))[arctan(e^u )+((shu)/(2ch^2 u))] F(u) = (1/(27))[arctan(chu+shu)+((shu)/(2(1+sh^2 u)))] F(x) = (1/(27))[arctan((x/3)+(√((x^2 /9)−1)))+(x/(6(1+(x^2 /9))))] F(x) = (1/(27))[arctan((x/3)+(√((x^2 /9)−1)))+((3x)/(2(x^2 +9)))]](https://www.tinkutara.com/question/Q136686.png)
$$\mathrm{F}\left({x}\right)\:=\:\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{2}} } \\ $$$$\mathrm{Let}\:{x}\:=\:\mathrm{3sh}{u} \\ $$$$\mathrm{F}\left({u}\right)\:=\:\int\frac{\mathrm{3ch}{u}}{\left(\mathrm{9sh}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{2}} }\:{du} \\ $$$$\mathrm{F}\left({u}\right)\:=\:\frac{\mathrm{1}}{\mathrm{27}}\int\frac{\mathrm{ch}{u}}{\mathrm{ch}^{\mathrm{4}} {u}}\:{du} \\ $$$$\mathrm{F}\left({u}\right)\:=\:\frac{\mathrm{1}}{\mathrm{27}}\int\frac{{du}}{\mathrm{ch}^{\mathrm{3}} {u}} \\ $$$$\mathrm{F}\left({u}\right)\:=\:\frac{\mathrm{1}}{\mathrm{27}}\int\frac{\mathrm{ch}^{\mathrm{2}} {u}−\mathrm{sh}^{\mathrm{2}} {u}}{\mathrm{ch}^{\mathrm{3}} {u}}\:{du} \\ $$$$\mathrm{F}\left({u}\right)\:=\:\frac{\mathrm{1}}{\mathrm{27}}\int\left(\frac{\mathrm{1}}{\mathrm{ch}{u}}−\mathrm{sh}{u}\frac{\mathrm{sh}{u}}{\mathrm{ch}^{\mathrm{3}} {u}}\right)\:{du} \\ $$$$\mathrm{F}\left({u}\right)\:=\:\frac{\mathrm{1}}{\mathrm{27}}\left[\mathrm{2arctan}\left({e}^{{u}} \right)+\mathrm{sh}{u}\frac{\mathrm{1}}{\mathrm{2ch}^{\mathrm{2}} {u}}\right. \\ $$$$+\int\mathrm{ch}{u}\left(−\frac{\mathrm{1}}{\mathrm{2ch}^{\mathrm{2}} {u}}\right){du} \\ $$$$\mathrm{F}\left({u}\right)\:=\:\frac{\mathrm{1}}{\mathrm{27}}\left[\mathrm{arctan}\left({e}^{{u}} \right)+\frac{\mathrm{sh}{u}}{\mathrm{2ch}^{\mathrm{2}} {u}}\right] \\ $$$$\mathrm{F}\left({u}\right)\:=\:\frac{\mathrm{1}}{\mathrm{27}}\left[\mathrm{arctan}\left(\mathrm{ch}{u}+\mathrm{sh}{u}\right)+\frac{\mathrm{sh}{u}}{\mathrm{2}\left(\mathrm{1}+\mathrm{sh}^{\mathrm{2}} {u}\right)}\right] \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{27}}\left[\mathrm{arctan}\left(\frac{{x}}{\mathrm{3}}+\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}\right)+\frac{{x}}{\mathrm{6}\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{9}}\right)}\right] \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{27}}\left[\mathrm{arctan}\left(\frac{{x}}{\mathrm{3}}+\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}\right)+\frac{\mathrm{3}{x}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{9}\right)}\right] \\ $$
Answered by mathmax by abdo last updated on 24/Mar/21
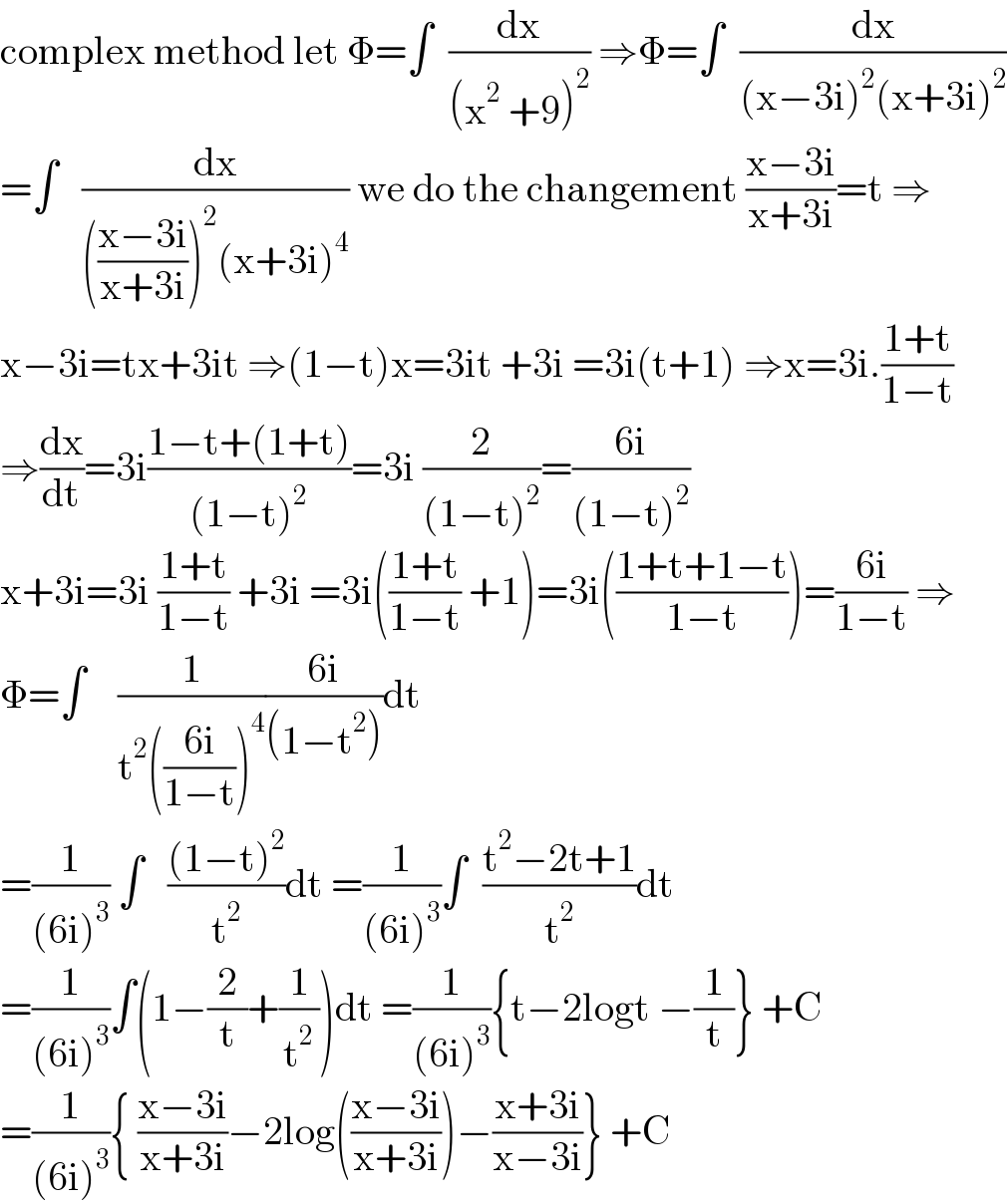
$$\mathrm{complex}\:\mathrm{method}\:\mathrm{let}\:\Phi=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{2}} }\:\Rightarrow\Phi=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{3i}\right)^{\mathrm{2}} \left(\mathrm{x}+\mathrm{3i}\right)^{\mathrm{2}} } \\ $$$$=\int\:\:\:\frac{\mathrm{dx}}{\left(\frac{\mathrm{x}−\mathrm{3i}}{\mathrm{x}+\mathrm{3i}}\right)^{\mathrm{2}} \left(\mathrm{x}+\mathrm{3i}\right)^{\mathrm{4}} }\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\frac{\mathrm{x}−\mathrm{3i}}{\mathrm{x}+\mathrm{3i}}=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{x}−\mathrm{3i}=\mathrm{tx}+\mathrm{3it}\:\Rightarrow\left(\mathrm{1}−\mathrm{t}\right)\mathrm{x}=\mathrm{3it}\:+\mathrm{3i}\:=\mathrm{3i}\left(\mathrm{t}+\mathrm{1}\right)\:\Rightarrow\mathrm{x}=\mathrm{3i}.\frac{\mathrm{1}+\mathrm{t}}{\mathrm{1}−\mathrm{t}} \\ $$$$\Rightarrow\frac{\mathrm{dx}}{\mathrm{dt}}=\mathrm{3i}\frac{\mathrm{1}−\mathrm{t}+\left(\mathrm{1}+\mathrm{t}\right)}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }=\mathrm{3i}\:\frac{\mathrm{2}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }=\frac{\mathrm{6i}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} } \\ $$$$\mathrm{x}+\mathrm{3i}=\mathrm{3i}\:\frac{\mathrm{1}+\mathrm{t}}{\mathrm{1}−\mathrm{t}}\:+\mathrm{3i}\:=\mathrm{3i}\left(\frac{\mathrm{1}+\mathrm{t}}{\mathrm{1}−\mathrm{t}}\:+\mathrm{1}\right)=\mathrm{3i}\left(\frac{\mathrm{1}+\mathrm{t}+\mathrm{1}−\mathrm{t}}{\mathrm{1}−\mathrm{t}}\right)=\frac{\mathrm{6i}}{\mathrm{1}−\mathrm{t}}\:\Rightarrow \\ $$$$\Phi=\int\:\:\:\:\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \left(\frac{\mathrm{6i}}{\mathrm{1}−\mathrm{t}}\right)^{\mathrm{4}} }\frac{\mathrm{6i}}{\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)}\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{6i}\right)^{\mathrm{3}} }\:\int\:\:\:\frac{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=\frac{\mathrm{1}}{\left(\mathrm{6i}\right)^{\mathrm{3}} }\int\:\:\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{2t}+\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{6i}\right)^{\mathrm{3}} }\int\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{t}}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\right)\mathrm{dt}\:=\frac{\mathrm{1}}{\left(\mathrm{6i}\right)^{\mathrm{3}} }\left\{\mathrm{t}−\mathrm{2logt}\:−\frac{\mathrm{1}}{\mathrm{t}}\right\}\:+\mathrm{C} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{6i}\right)^{\mathrm{3}} }\left\{\:\frac{\mathrm{x}−\mathrm{3i}}{\mathrm{x}+\mathrm{3i}}−\mathrm{2log}\left(\frac{\mathrm{x}−\mathrm{3i}}{\mathrm{x}+\mathrm{3i}}\right)−\frac{\mathrm{x}+\mathrm{3i}}{\mathrm{x}−\mathrm{3i}}\right\}\:+\mathrm{C} \\ $$
Commented by mathmax by abdo last updated on 24/Mar/21

$$\mathrm{parametric}\:\mathrm{method}\:\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }\:\:\:\:\:\left(\mathrm{a}>\mathrm{0}\right) \\ $$$$\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)\:=−\mathrm{2a}\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{3}\right)=−\mathrm{6}\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{2}} } \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=_{\mathrm{x}=\mathrm{at}} \:\:\int\:\:\frac{\mathrm{adt}}{\mathrm{a}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\mathrm{a}}\:\mathrm{arctan}\left(\mathrm{t}\right)\:+\mathrm{C}=\frac{\mathrm{1}}{\mathrm{a}}\mathrm{arctan}\left(\frac{\mathrm{x}}{\mathrm{a}}\right)\:+\mathrm{C} \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=−\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\mathrm{arctan}\left(\frac{\mathrm{x}}{\mathrm{a}}\right)+\frac{\mathrm{1}}{\mathrm{a}}×\frac{\mathrm{1}}{\mathrm{a}\left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }\right)} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\mathrm{arctan}\left(\frac{\mathrm{x}}{\mathrm{a}}\right)\:+\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{3}\right)\:=−\frac{\mathrm{1}}{\mathrm{9}}\mathrm{arctan}\left(\frac{\mathrm{x}}{\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}}\:\mathrm{and} \\ $$$$\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{f}^{'} \left(\mathrm{3}\right)=−\frac{\mathrm{1}}{\mathrm{6}}\left(−\frac{\mathrm{1}}{\mathrm{9}}\:\mathrm{arctan}\left(\frac{\mathrm{x}}{\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}}\right)+\mathrm{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{54}}\mathrm{arctan}\left(\frac{\mathrm{x}}{\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{6}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)}\:+\mathrm{c} \\ $$$$ \\ $$
