Question Number 136793 by JulioCesar last updated on 26/Mar/21

Answered by Dwaipayan Shikari last updated on 26/Mar/21
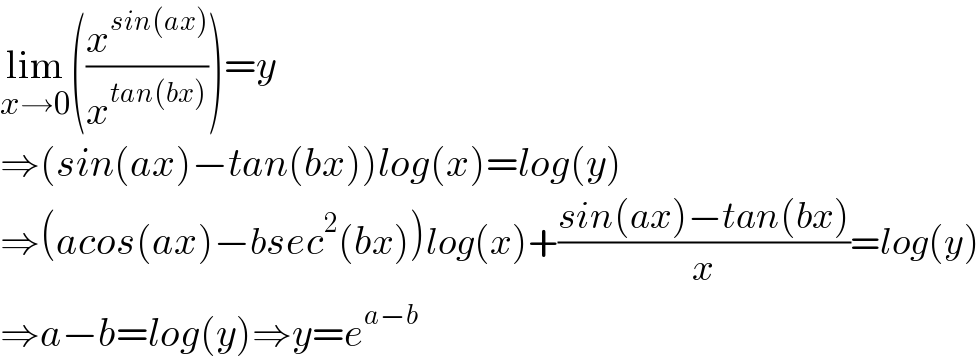
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{x}^{{sin}\left({ax}\right)} }{{x}^{{tan}\left({bx}\right)} }\right)={y} \\ $$$$\Rightarrow\left({sin}\left({ax}\right)−{tan}\left({bx}\right)\right){log}\left({x}\right)={log}\left({y}\right) \\ $$$$\Rightarrow\left({acos}\left({ax}\right)−{bsec}^{\mathrm{2}} \left({bx}\right)\right){log}\left({x}\right)+\frac{{sin}\left({ax}\right)−{tan}\left({bx}\right)}{{x}}={log}\left({y}\right) \\ $$$$\Rightarrow{a}−{b}={log}\left({y}\right)\Rightarrow{y}={e}^{{a}−{b}} \\ $$
