Menu Close

Question-136815

Tinku Tara 0 Comments
Pin




Question Number 136815 by rs4089 last updated on 26/Mar/21
Answered by Dwaipayan Shikari last updated on 26/Mar/21
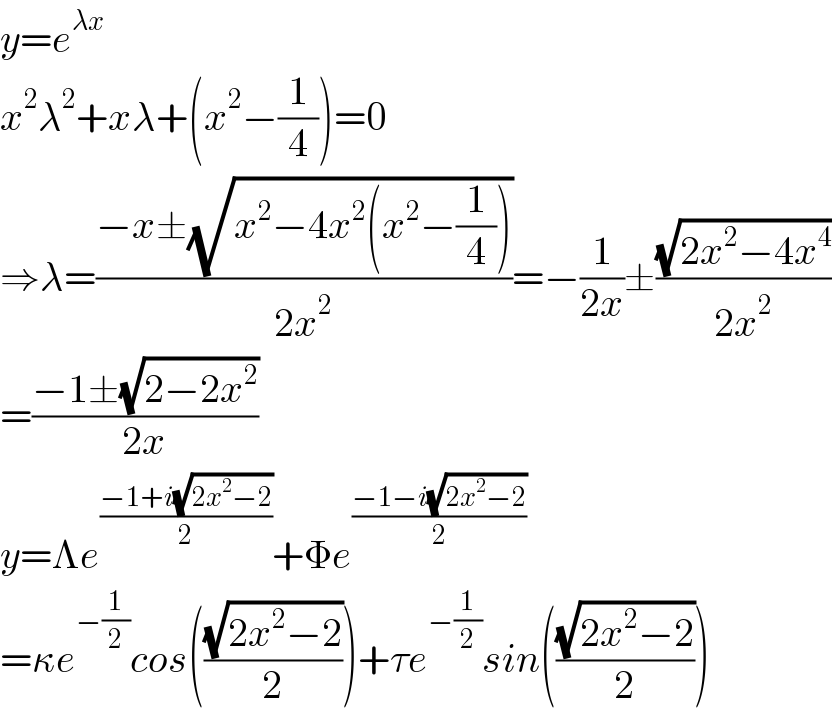
y=e^(λx) x^2 λ^2 +xλ+(x^2 −(1/4))=0 ⇒λ=((−x±(√(x^2 −4x^2 (x^2 −(1/4)))))/(2x^2 ))=−(1/(2x))±((√(2x^2 −4x^4 ))/(2x^2 )) =((−1±(√(2−2x^2 )))/(2x)) y=Λe^((−1+i(√(2x^2 −2)))/2) +Φe^((−1−i(√(2x^2 −2)))/2) =κe^(−(1/2)) cos(((√(2x^2 −2))/2))+τe^(−(1/2)) sin(((√(2x^2 −2))/2))
$${y}={e}^{\lambda{x}} \\ $$$${x}^{\mathrm{2}} \lambda^{\mathrm{2}} +{x}\lambda+\left({x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\right)=\mathrm{0} \\ $$$$\Rightarrow\lambda=\frac{−{x}\pm\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\right)}}{\mathrm{2}{x}^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{2}{x}}\pm\frac{\sqrt{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{4}} }}{\mathrm{2}{x}^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{1}\pm\sqrt{\mathrm{2}−\mathrm{2}{x}^{\mathrm{2}} }}{\mathrm{2}{x}} \\ $$$${y}=\Lambda{e}^{\frac{−\mathrm{1}+{i}\sqrt{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}}}{\mathrm{2}}} +\Phi{e}^{\frac{−\mathrm{1}−{i}\sqrt{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}}}{\mathrm{2}}} \\ $$$$=\kappa{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} {cos}\left(\frac{\sqrt{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}}}{\mathrm{2}}\right)+\tau{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} {sin}\left(\frac{\sqrt{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}}}{\mathrm{2}}\right) \\ $$
Answered by Olaf last updated on 26/Mar/21
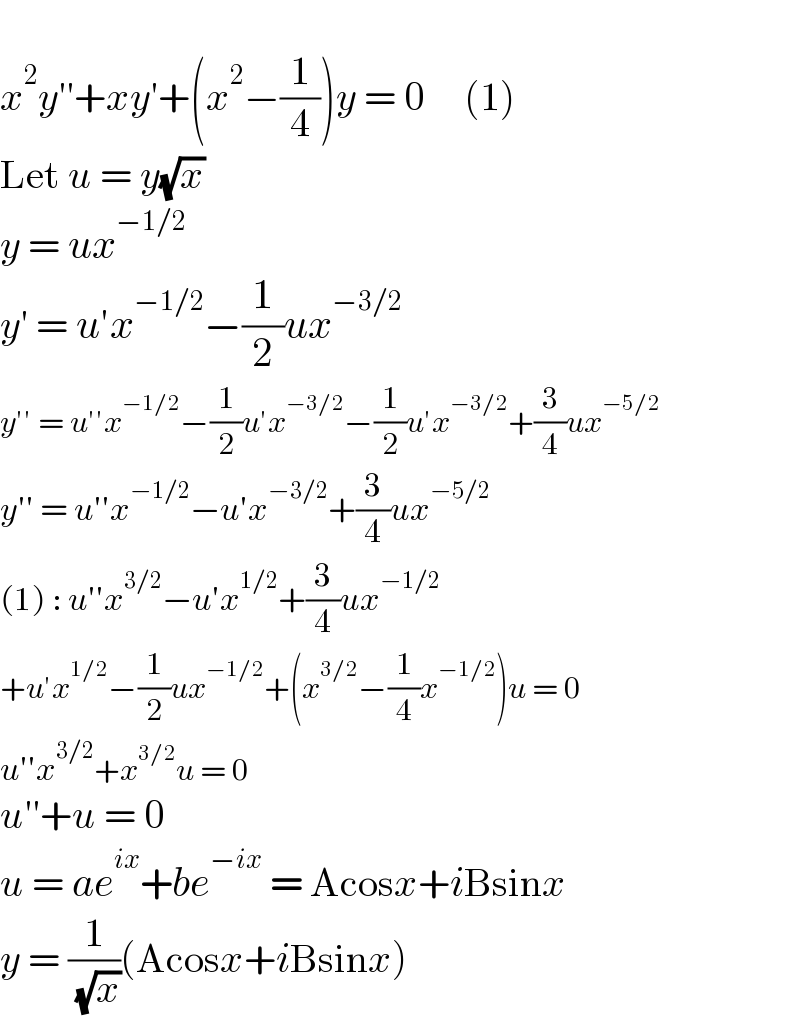
x^2 y′′+xy′+(x^2 −(1/4))y = 0 (1) Let u = y(√x) y = ux^(−1/2) y′ = u′x^(−1/2) −(1/2)ux^(−3/2) y′′ = u′′x^(−1/2) −(1/2)u′x^(−3/2) −(1/2)u′x^(−3/2) +(3/4)ux^(−5/2) y′′ = u′′x^(−1/2) −u′x^(−3/2) +(3/4)ux^(−5/2) (1) : u′′x^(3/2) −u′x^(1/2) +(3/4)ux^(−1/2) +u′x^(1/2) −(1/2)ux^(−1/2) +(x^(3/2) −(1/4)x^(−1/2) )u = 0 u′′x^(3/2) +x^(3/2) u = 0 u′′+u = 0 u = ae^(ix) +be^(−ix) = Acosx+iBsinx y = (1/( (√x)))(Acosx+iBsinx)
$$ \\ $$$${x}^{\mathrm{2}} {y}''+{xy}'+\left({x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\right){y}\:=\:\mathrm{0}\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{Let}\:{u}\:=\:{y}\sqrt{{x}} \\ $$$${y}\:=\:{ux}^{−\mathrm{1}/\mathrm{2}} \\ $$$${y}'\:=\:{u}'{x}^{−\mathrm{1}/\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}{ux}^{−\mathrm{3}/\mathrm{2}} \\ $$$${y}''\:=\:{u}''{x}^{−\mathrm{1}/\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}{u}'{x}^{−\mathrm{3}/\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}{u}'{x}^{−\mathrm{3}/\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}{ux}^{−\mathrm{5}/\mathrm{2}} \\ $$$${y}''\:=\:{u}''{x}^{−\mathrm{1}/\mathrm{2}} −{u}'{x}^{−\mathrm{3}/\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}{ux}^{−\mathrm{5}/\mathrm{2}} \\ $$$$\left(\mathrm{1}\right)\::\:{u}''{x}^{\mathrm{3}/\mathrm{2}} −{u}'{x}^{\mathrm{1}/\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}{ux}^{−\mathrm{1}/\mathrm{2}} \\ $$$$+{u}'{x}^{\mathrm{1}/\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}{ux}^{−\mathrm{1}/\mathrm{2}} +\left({x}^{\mathrm{3}/\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}{x}^{−\mathrm{1}/\mathrm{2}} \right){u}\:=\:\mathrm{0} \\ $$$${u}''{x}^{\mathrm{3}/\mathrm{2}} +{x}^{\mathrm{3}/\mathrm{2}} {u}\:=\:\mathrm{0} \\ $$$${u}''+{u}\:=\:\mathrm{0} \\ $$$${u}\:=\:{ae}^{{ix}} +{be}^{−{ix}} \:=\:\mathrm{Acos}{x}+{i}\mathrm{Bsin}{x} \\ $$$${y}\:=\:\frac{\mathrm{1}}{\:\sqrt{{x}}}\left(\mathrm{Acos}{x}+{i}\mathrm{Bsin}{x}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *