Question Number 136897 by mohammad17 last updated on 27/Mar/21
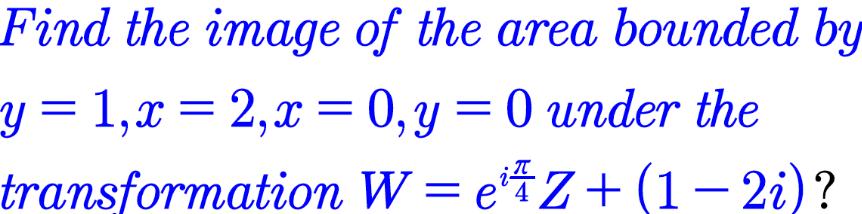
Answered by Olaf last updated on 27/Mar/21

$$ \\ $$$${f}\left({z}\right)\:=\:{e}^{{i}\frac{\pi}{\mathrm{4}}} {z}+\left(\mathrm{1}−\mathrm{2}{i}\right) \\ $$$${f}\left({z}\right)−{z}_{\mathrm{0}} \:=\:{e}^{{i}\frac{\pi}{\mathrm{4}}} \left({z}−{z}_{\mathrm{0}} \right)+\left({e}^{{i}\frac{\pi}{\mathrm{4}}} −\mathrm{1}\right){z}_{\mathrm{0}} +\left(\mathrm{1}−\mathrm{2}{i}\right) \\ $$$$\mathrm{We}\:\mathrm{choose}\:{z}_{\mathrm{0}} \:\mathrm{such}\:\mathrm{as}\::\:\left({e}^{{i}\frac{\pi}{\mathrm{4}}} −\mathrm{1}\right){z}_{\mathrm{0}} +\left(\mathrm{1}−\mathrm{2}{i}\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{z}_{\mathrm{0}} \:=\:−\frac{\mathrm{1}−\mathrm{2}{i}}{{e}^{{i}\frac{\pi}{\mathrm{4}}} −\mathrm{1}}\:=\:−\frac{\mathrm{1}−\mathrm{2}{i}}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\mathrm{1}+\frac{{i}}{\:\sqrt{\mathrm{2}}}}\:=−\frac{\sqrt{\mathrm{2}}+\left(\mathrm{2}−\sqrt{\mathrm{2}}\right){i}}{\mathrm{2}−\sqrt{\mathrm{2}}} \\ $$$${z}_{\mathrm{0}} \:=\:−\:\frac{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\mathrm{1}−\sqrt{\mathrm{2}}+\left(\mathrm{2}−\sqrt{\mathrm{2}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right){i}}{\mathrm{2}−\sqrt{\mathrm{2}}}\:=\:\left(\frac{\mathrm{3}}{\mathrm{2}}+\sqrt{\mathrm{2}}\right)−\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{2}}{i} \\ $$$${f}\left({z}\right)−{z}_{\mathrm{0}} \:=\:{e}^{{i}\frac{\pi}{\mathrm{4}}} \left({z}−{z}_{\mathrm{0}} \right) \\ $$$$\mathrm{The}\:\mathrm{transformation}\:\mathrm{W}\:\mathrm{is}\:\mathrm{the}\:\mathrm{rotation} \\ $$$$\mathrm{angle}\:\frac{\pi}{\mathrm{4}}\:\mathrm{around}\:\mathrm{the}\:\mathrm{point}\:{z}_{\mathrm{0}} . \\ $$$$\mathrm{The}\:\mathrm{area}\:\mathcal{A}\:=\:\left\{\mathrm{0}\leqslant{x}\leqslant\mathrm{2},\:\mathrm{0}\leqslant{y}\leqslant\mathrm{1}\right\}\:\mathrm{is}\:\mathrm{a} \\ $$$$\mathrm{rectangle}\:\mathrm{O},\mathrm{A}\left(\mathrm{2}\right),\mathrm{B}\left(\mathrm{2}+{i}\right),\mathrm{C}\left({i}\right) \\ $$$$\mathrm{The}\:\mathrm{image}\:\mathcal{A}'\:\mathrm{of}\:\mathcal{A}\:\mathrm{by}\:\mathrm{W}\:\mathrm{is}\:\mathrm{another} \\ $$$$\mathrm{rectangle}\:\mathrm{O}'\mathrm{A}'\mathrm{B}'\mathrm{C}' \\ $$$$\mathrm{O}'\:=\:{f}\left(\mathrm{O}\right)\:=\:\mathrm{1}−\mathrm{2}{i} \\ $$$$\mathrm{A}'\:=\:{f}\left(\mathrm{A}\right)\:=\:\mathrm{2}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{1}+{i}\right)+\left(\mathrm{1}−\mathrm{2}{i}\right)\:=\:\sqrt{\mathrm{2}}+\mathrm{1}+\left(\sqrt{\mathrm{2}}−\mathrm{2}\right){i} \\ $$$$\mathrm{B}'\:=\:{f}\left(\mathrm{B}\right)\:=\:\left(\mathrm{2}+{i}\right)\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{1}+{i}\right)+\left(\mathrm{1}−\mathrm{2}{i}\right)\:=\:\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}−\mathrm{2}\right){i} \\ $$$$\mathrm{C}'\:=\:{f}\left(\mathrm{C}\right)\:=\:{i}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{1}+{i}\right)+\left(\mathrm{1}−\mathrm{2}{i}\right)\:=\:\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\mathrm{2}\right){i} \\ $$
