Question Number 137065 by mr W last updated on 29/Mar/21

Commented by mr W last updated on 29/Mar/21
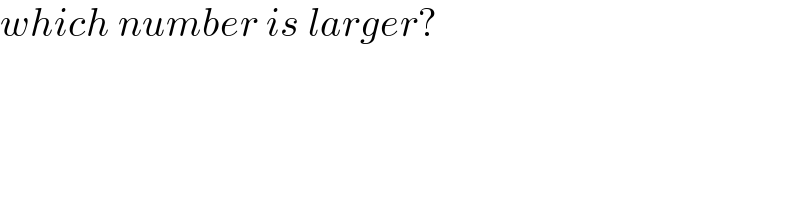
$${which}\:{number}\:{is}\:{larger}? \\ $$
Answered by mr W last updated on 30/Mar/21
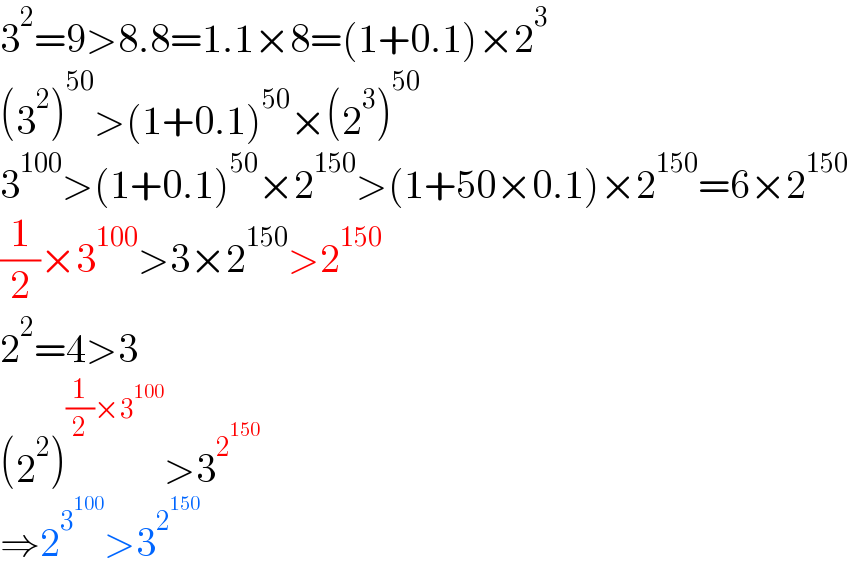
$$\mathrm{3}^{\mathrm{2}} =\mathrm{9}>\mathrm{8}.\mathrm{8}=\mathrm{1}.\mathrm{1}×\mathrm{8}=\left(\mathrm{1}+\mathrm{0}.\mathrm{1}\right)×\mathrm{2}^{\mathrm{3}} \\ $$$$\left(\mathrm{3}^{\mathrm{2}} \right)^{\mathrm{50}} >\left(\mathrm{1}+\mathrm{0}.\mathrm{1}\right)^{\mathrm{50}} ×\left(\mathrm{2}^{\mathrm{3}} \right)^{\mathrm{50}} \\ $$$$\mathrm{3}^{\mathrm{100}} >\left(\mathrm{1}+\mathrm{0}.\mathrm{1}\right)^{\mathrm{50}} ×\mathrm{2}^{\mathrm{150}} >\left(\mathrm{1}+\mathrm{50}×\mathrm{0}.\mathrm{1}\right)×\mathrm{2}^{\mathrm{150}} =\mathrm{6}×\mathrm{2}^{\mathrm{150}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{3}^{\mathrm{100}} >\mathrm{3}×\mathrm{2}^{\mathrm{150}} >\mathrm{2}^{\mathrm{150}} \\ $$$$\mathrm{2}^{\mathrm{2}} =\mathrm{4}>\mathrm{3} \\ $$$$\left(\mathrm{2}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{3}^{\mathrm{100}} } >\mathrm{3}^{\mathrm{2}^{\mathrm{150}} } \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{3}^{\mathrm{100}} } >\mathrm{3}^{\mathrm{2}^{\mathrm{150}} } \\ $$
