Menu Close

Question-137069

Tinku Tara 0 Comments
Pin




Question Number 137069 by 0731619177 last updated on 29/Mar/21
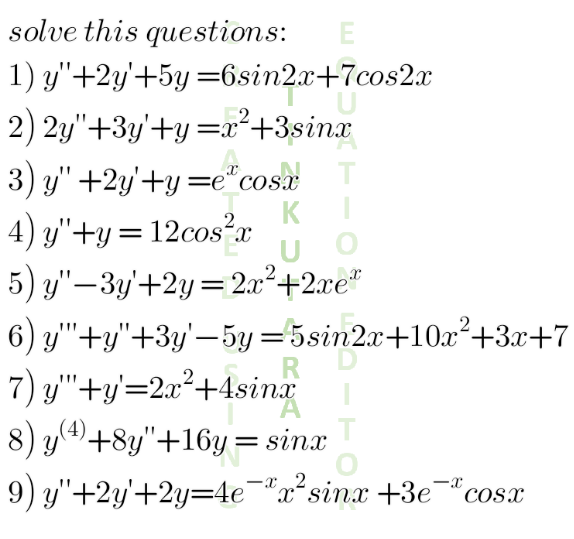
Answered by Ñï= last updated on 29/Mar/21
(1)y_p =(1/(D^2 +2D+5))(6sin 2x+7cos 2x) =(1/(2D+1))(6sin 2x+7cos 2x)=(((1+2D))/9)(6sin 2x+7cos 2x) =(1/9)(31cos 2x−22sin 2x) y=e^(−x) (C_1 sin 2x+C_2 cos 2x)+(1/9)(31cos 2x−22sin 2x) (3)y_p =(1/(D^2 +2D+1))e^x cos x=e^x (1/(4D+3))cos x=e^x ((3−4D)/(25))cos x =e^x ((3/(25))cos x+(4/(25))sin x) y=(C_1 +xC_2 )e^x +e^x ((3/(25))cos x+(4/(25))sin x) (9)y_p =(1/(D^2 +2D+2))(4e^(−x) x^2 sin x+3e^(−x) cos x) =e^(−x) (1/(D^2 +1))(4x^2 sin x+3cos x) =(2/i)e^(−x) (1/(D^2 +1))x^2 (e^(ix) −e^(−ix) )+xe^(−x) (3/((D^2 +1)′))cos x =(2/i)e^(−x) {e^(ix) (1/((D+i)^2 +1))x^2 −e^(−ix) (1/((D−i)^2 +1))x^2 }+(3/2)xe^(−x) sin x =(2/i)e^(−x) {e^(ix) (1/(D^2 +2iD))x^2 −e^(−ix) (1/(D^2 −2iD))x^2 }+(3/2)xe^(−x) sin x =(2/(3i))e^(−x) {e^(ix) (1/(D+2i))x^3 −e^(−ix) (1/(D−2i))x^3 }+(3/2)xe^(−x) sin x =−(1/3)e^(−x) {e^(ix) (1−(D/(2i))−(D^2 /4)+(D^3 /(8i)))x^3 +e^(−ix) (1+(D/(2i))−(D^2 /4)−(D^3 /(8i)))x^3 }+(3/2)xe^(−x) sin x =−(1/3)e^(−x) {e^(ix) (x^3 −(3/(2i))x^2 −(3/2)x+(3/(4i)))+e^(−ix) (x^3 +(3/(2i))x^2 −(3/2)x−(3/(4i)))}+(3/2)xe^(−x) sin x =−(1/3)e^(−x) (2x^3 cos x−3x^2 sin x−3xcos x+(3/2)sin x)+(3/2)xe^(−x) sin x y=e^(−x) (C_1 sin x+C_2 cos x)−(1/3)e^(−x) (2x^3 cos x−3x^2 sin x−3xcos x)+(3/2)xe^(−x) sin x
$$\left(\mathrm{1}\right){y}_{{p}} =\frac{\mathrm{1}}{{D}^{\mathrm{2}} +\mathrm{2}{D}+\mathrm{5}}\left(\mathrm{6sin}\:\mathrm{2}{x}+\mathrm{7cos}\:\mathrm{2}{x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{D}+\mathrm{1}}\left(\mathrm{6sin}\:\mathrm{2}{x}+\mathrm{7cos}\:\mathrm{2}{x}\right)=\frac{\left(\mathrm{1}+\mathrm{2}{D}\right)}{\mathrm{9}}\left(\mathrm{6sin}\:\mathrm{2}\boldsymbol{{x}}+\mathrm{7cos}\:\mathrm{2}{x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{31cos}\:\mathrm{2}{x}−\mathrm{22sin}\:\mathrm{2}{x}\right) \\ $$$${y}={e}^{−{x}} \left({C}_{\mathrm{1}} \mathrm{sin}\:\mathrm{2}{x}+{C}_{\mathrm{2}} \mathrm{cos}\:\mathrm{2}{x}\right)+\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{31cos}\:\mathrm{2}{x}−\mathrm{22sin}\:\mathrm{2}{x}\right) \\ $$$$\left(\mathrm{3}\right){y}_{{p}} =\frac{\mathrm{1}}{{D}^{\mathrm{2}} +\mathrm{2}{D}+\mathrm{1}}{e}^{{x}} \mathrm{cos}\:{x}={e}^{{x}} \frac{\mathrm{1}}{\mathrm{4}{D}+\mathrm{3}}\mathrm{cos}\:{x}={e}^{{x}} \frac{\mathrm{3}−\mathrm{4}{D}}{\mathrm{25}}\mathrm{cos}\:{x} \\ $$$$={e}^{{x}} \left(\frac{\mathrm{3}}{\mathrm{25}}\mathrm{cos}\:{x}+\frac{\mathrm{4}}{\mathrm{25}}\mathrm{sin}\:{x}\right) \\ $$$${y}=\left({C}_{\mathrm{1}} +{xC}_{\mathrm{2}} \right){e}^{{x}} +{e}^{{x}} \left(\frac{\mathrm{3}}{\mathrm{25}}\mathrm{cos}\:{x}+\frac{\mathrm{4}}{\mathrm{25}}\mathrm{sin}\:{x}\right) \\ $$$$\left(\mathrm{9}\right){y}_{{p}} =\frac{\mathrm{1}}{{D}^{\mathrm{2}} +\mathrm{2}{D}+\mathrm{2}}\left(\mathrm{4}{e}^{−{x}} {x}^{\mathrm{2}} \mathrm{sin}\:{x}+\mathrm{3}{e}^{−{x}} \mathrm{cos}\:{x}\right) \\ $$$$={e}^{−{x}} \frac{\mathrm{1}}{{D}^{\mathrm{2}} +\mathrm{1}}\left(\mathrm{4}{x}^{\mathrm{2}} \mathrm{sin}\:{x}+\mathrm{3cos}\:{x}\right) \\ $$$$=\frac{\mathrm{2}}{{i}}{e}^{−{x}} \frac{\mathrm{1}}{{D}^{\mathrm{2}} +\mathrm{1}}{x}^{\mathrm{2}} \left({e}^{{ix}} −{e}^{−{ix}} \right)+{xe}^{−{x}} \frac{\mathrm{3}}{\left({D}^{\mathrm{2}} +\mathrm{1}\right)'}\mathrm{cos}\:{x} \\ $$$$=\frac{\mathrm{2}}{{i}}{e}^{−{x}} \left\{{e}^{{ix}} \frac{\mathrm{1}}{\left({D}+{i}\right)^{\mathrm{2}} +\mathrm{1}}{x}^{\mathrm{2}} −{e}^{−{ix}} \frac{\mathrm{1}}{\left({D}−{i}\right)^{\mathrm{2}} +\mathrm{1}}{x}^{\mathrm{2}} \right\}+\frac{\mathrm{3}}{\mathrm{2}}{xe}^{−{x}} \mathrm{sin}\:{x} \\ $$$$=\frac{\mathrm{2}}{{i}}{e}^{−{x}} \left\{{e}^{{ix}} \frac{\mathrm{1}}{{D}^{\mathrm{2}} +\mathrm{2}{iD}}{x}^{\mathrm{2}} −{e}^{−{ix}} \frac{\mathrm{1}}{{D}^{\mathrm{2}} −\mathrm{2}{iD}}{x}^{\mathrm{2}} \right\}+\frac{\mathrm{3}}{\mathrm{2}}{xe}^{−{x}} \mathrm{sin}\:{x} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}{i}}{e}^{−{x}} \left\{{e}^{{ix}} \frac{\mathrm{1}}{{D}+\mathrm{2}{i}}{x}^{\mathrm{3}} −{e}^{−{ix}} \frac{\mathrm{1}}{{D}−\mathrm{2}{i}}{x}^{\mathrm{3}} \right\}+\frac{\mathrm{3}}{\mathrm{2}}{xe}^{−{x}} \mathrm{sin}\:{x} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}{e}^{−{x}} \left\{{e}^{{ix}} \left(\mathrm{1}−\frac{{D}}{\mathrm{2}{i}}−\frac{{D}^{\mathrm{2}} }{\mathrm{4}}+\frac{{D}^{\mathrm{3}} }{\mathrm{8}{i}}\right){x}^{\mathrm{3}} +{e}^{−{ix}} \left(\mathrm{1}+\frac{{D}}{\mathrm{2}{i}}−\frac{{D}^{\mathrm{2}} }{\mathrm{4}}−\frac{{D}^{\mathrm{3}} }{\mathrm{8}{i}}\right){x}^{\mathrm{3}} \right\}+\frac{\mathrm{3}}{\mathrm{2}}{xe}^{−{x}} \mathrm{sin}\:{x} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}{e}^{−{x}} \left\{{e}^{{ix}} \left({x}^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{2}{i}}{x}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}}{x}+\frac{\mathrm{3}}{\mathrm{4}{i}}\right)+{e}^{−{ix}} \left({x}^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{2}{i}}{x}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}}{x}−\frac{\mathrm{3}}{\mathrm{4}{i}}\right)\right\}+\frac{\mathrm{3}}{\mathrm{2}}{xe}^{−{x}} \mathrm{sin}\:{x} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}{e}^{−{x}} \left(\mathrm{2}{x}^{\mathrm{3}} \mathrm{cos}\:{x}−\mathrm{3}{x}^{\mathrm{2}} \mathrm{sin}\:{x}−\mathrm{3}{x}\mathrm{cos}\:{x}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{sin}\:{x}\right)+\frac{\mathrm{3}}{\mathrm{2}}{xe}^{−{x}} \mathrm{sin}\:{x} \\ $$$${y}={e}^{−{x}} \left({C}_{\mathrm{1}} \mathrm{sin}\:{x}+{C}_{\mathrm{2}} \mathrm{cos}\:{x}\right)−\frac{\mathrm{1}}{\mathrm{3}}{e}^{−{x}} \left(\mathrm{2}{x}^{\mathrm{3}} \mathrm{cos}\:{x}−\mathrm{3}{x}^{\mathrm{2}} \mathrm{sin}\:{x}−\mathrm{3}{x}\mathrm{cos}\:{x}\right)+\frac{\mathrm{3}}{\mathrm{2}}{xe}^{−{x}} \mathrm{sin}\:{x} \\ $$
Answered by Ñï= last updated on 29/Mar/21
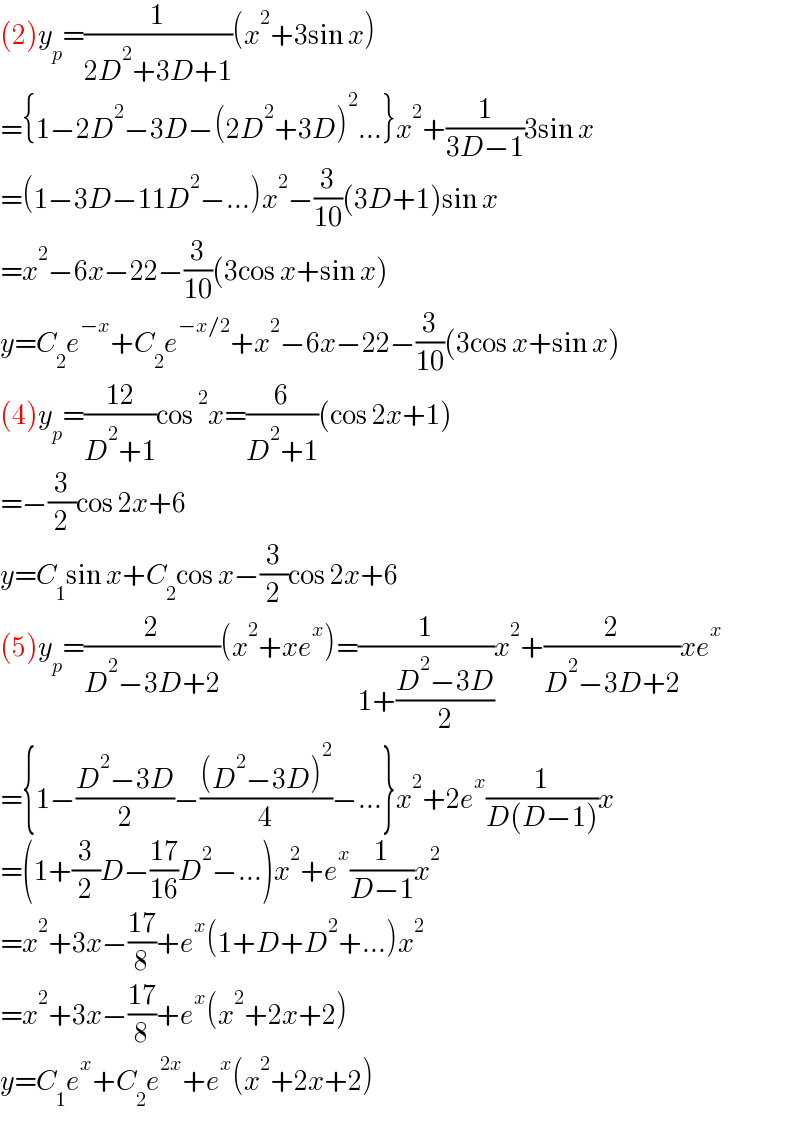
(2)y_p =(1/(2D^2 +3D+1))(x^2 +3sin x) ={1−2D^2 −3D−(2D^2 +3D)^2 ...}x^2 +(1/(3D−1))3sin x =(1−3D−11D^2 −...)x^2 −(3/(10))(3D+1)sin x =x^2 −6x−22−(3/(10))(3cos x+sin x) y=C_2 e^(−x) +C_2 e^(−x/2) +x^2 −6x−22−(3/(10))(3cos x+sin x) (4)y_p =((12)/(D^2 +1))cos^2 x=(6/(D^2 +1))(cos 2x+1) =−(3/2)cos 2x+6 y=C_1 sin x+C_2 cos x−(3/2)cos 2x+6 (5)y_p =(2/(D^2 −3D+2))(x^2 +xe^x )=(1/(1+((D^2 −3D)/2)))x^2 +(2/(D^2 −3D+2))xe^x ={1−((D^2 −3D)/2)−(((D^2 −3D)^2 )/4)−...}x^2 +2e^x (1/(D(D−1)))x =(1+(3/2)D−((17)/(16))D^2 −...)x^2 +e^x (1/(D−1))x^2 =x^2 +3x−((17)/8)+e^x (1+D+D^2 +...)x^2 =x^2 +3x−((17)/8)+e^x (x^2 +2x+2) y=C_1 e^x +C_2 e^(2x) +e^x (x^2 +2x+2)
$$\left(\mathrm{2}\right){y}_{{p}} =\frac{\mathrm{1}}{\mathrm{2}{D}^{\mathrm{2}} +\mathrm{3}{D}+\mathrm{1}}\left({x}^{\mathrm{2}} +\mathrm{3sin}\:{x}\right) \\ $$$$=\left\{\mathrm{1}−\mathrm{2}{D}^{\mathrm{2}} −\mathrm{3}{D}−\left(\mathrm{2}{D}^{\mathrm{2}} +\mathrm{3}{D}\right)^{\mathrm{2}} …\right\}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}{D}−\mathrm{1}}\mathrm{3sin}\:{x} \\ $$$$=\left(\mathrm{1}−\mathrm{3}{D}−\mathrm{11}{D}^{\mathrm{2}} −…\right){x}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{10}}\left(\mathrm{3}{D}+\mathrm{1}\right)\mathrm{sin}\:{x} \\ $$$$={x}^{\mathrm{2}} −\mathrm{6}{x}−\mathrm{22}−\frac{\mathrm{3}}{\mathrm{10}}\left(\mathrm{3cos}\:{x}+\mathrm{sin}\:{x}\right) \\ $$$${y}={C}_{\mathrm{2}} {e}^{−{x}} +{C}_{\mathrm{2}} {e}^{−{x}/\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{6}{x}−\mathrm{22}−\frac{\mathrm{3}}{\mathrm{10}}\left(\mathrm{3cos}\:{x}+\mathrm{sin}\:{x}\right) \\ $$$$\left(\mathrm{4}\right){y}_{{p}} =\frac{\mathrm{12}}{{D}^{\mathrm{2}} +\mathrm{1}}\mathrm{cos}\:^{\mathrm{2}} {x}=\frac{\mathrm{6}}{{D}^{\mathrm{2}} +\mathrm{1}}\left(\mathrm{cos}\:\mathrm{2}{x}+\mathrm{1}\right) \\ $$$$=−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{x}+\mathrm{6} \\ $$$${y}={C}_{\mathrm{1}} \mathrm{sin}\:{x}+{C}_{\mathrm{2}} \mathrm{cos}\:{x}−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{x}+\mathrm{6} \\ $$$$\left(\mathrm{5}\right){y}_{{p}} =\frac{\mathrm{2}}{{D}^{\mathrm{2}} −\mathrm{3}{D}+\mathrm{2}}\left({x}^{\mathrm{2}} +{xe}^{{x}} \right)=\frac{\mathrm{1}}{\mathrm{1}+\frac{{D}^{\mathrm{2}} −\mathrm{3}{D}}{\mathrm{2}}}{x}^{\mathrm{2}} +\frac{\mathrm{2}}{{D}^{\mathrm{2}} −\mathrm{3}{D}+\mathrm{2}}{xe}^{{x}} \\ $$$$=\left\{\mathrm{1}−\frac{{D}^{\mathrm{2}} −\mathrm{3}{D}}{\mathrm{2}}−\frac{\left({D}^{\mathrm{2}} −\mathrm{3}{D}\right)^{\mathrm{2}} }{\mathrm{4}}−…\right\}{x}^{\mathrm{2}} +\mathrm{2}{e}^{{x}} \frac{\mathrm{1}}{{D}\left({D}−\mathrm{1}\right)}{x} \\ $$$$=\left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}{D}−\frac{\mathrm{17}}{\mathrm{16}}{D}^{\mathrm{2}} −…\right){x}^{\mathrm{2}} +{e}^{{x}} \frac{\mathrm{1}}{{D}−\mathrm{1}}{x}^{\mathrm{2}} \\ $$$$={x}^{\mathrm{2}} +\mathrm{3}{x}−\frac{\mathrm{17}}{\mathrm{8}}+{e}^{{x}} \left(\mathrm{1}+{D}+{D}^{\mathrm{2}} +…\right){x}^{\mathrm{2}} \\ $$$$={x}^{\mathrm{2}} +\mathrm{3}{x}−\frac{\mathrm{17}}{\mathrm{8}}+{e}^{{x}} \left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right) \\ $$$${y}={C}_{\mathrm{1}} {e}^{{x}} +{C}_{\mathrm{2}} {e}^{\mathrm{2}{x}} +{e}^{{x}} \left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right) \\ $$
Answered by Ñï= last updated on 29/Mar/21
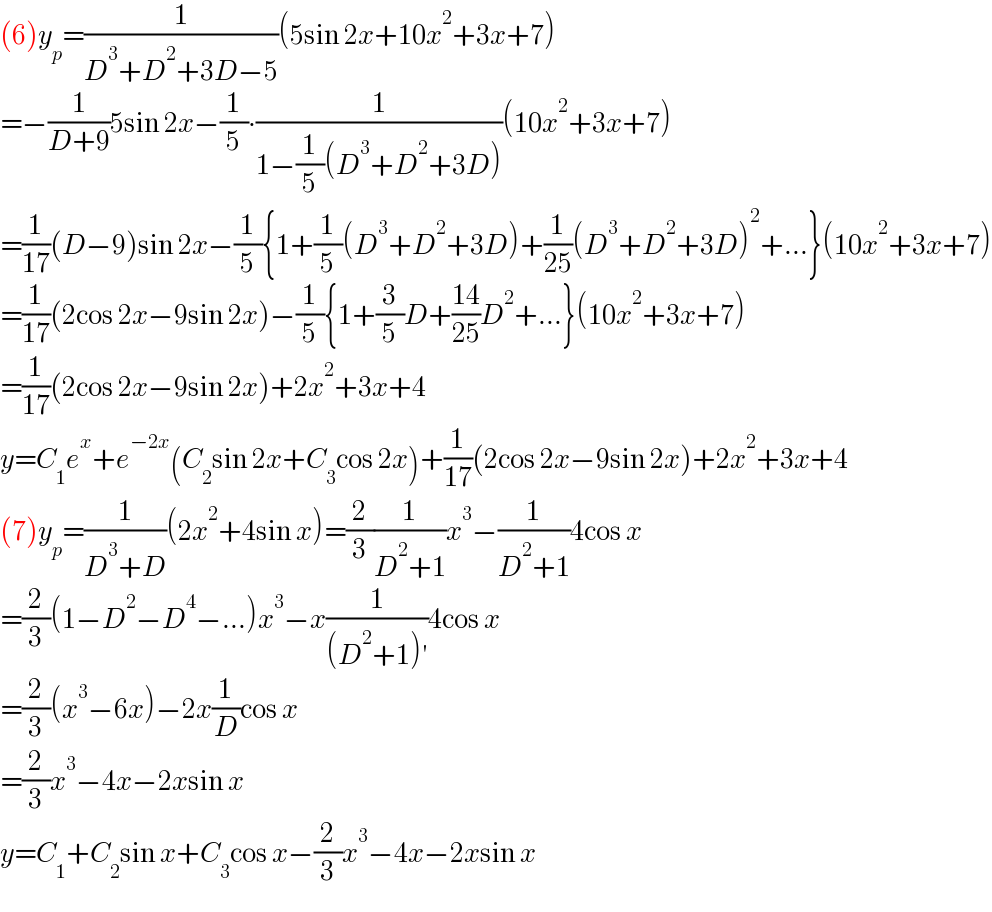
(6)y_p =(1/(D^3 +D^2 +3D−5))(5sin 2x+10x^2 +3x+7) =−(1/(D+9))5sin 2x−(1/5)∙(1/(1−(1/5)(D^3 +D^2 +3D)))(10x^2 +3x+7) =(1/(17))(D−9)sin 2x−(1/5){1+(1/5)(D^3 +D^2 +3D)+(1/(25))(D^3 +D^2 +3D)^2 +...}(10x^2 +3x+7) =(1/(17))(2cos 2x−9sin 2x)−(1/5){1+(3/5)D+((14)/(25))D^2 +...}(10x^2 +3x+7) =(1/(17))(2cos 2x−9sin 2x)+2x^2 +3x+4 y=C_1 e^x +e^(−2x) (C_2 sin 2x+C_3 cos 2x)+(1/(17))(2cos 2x−9sin 2x)+2x^2 +3x+4 (7)y_p =(1/(D^3 +D))(2x^2 +4sin x)=(2/3)(1/(D^2 +1))x^3 −(1/(D^2 +1))4cos x =(2/3)(1−D^2 −D^4 −...)x^3 −x(1/((D^2 +1)′))4cos x =(2/3)(x^3 −6x)−2x(1/D)cos x =(2/3)x^3 −4x−2xsin x y=C_1 +C_2 sin x+C_3 cos x−(2/3)x^3 −4x−2xsin x
$$\left(\mathrm{6}\right){y}_{{p}} =\frac{\mathrm{1}}{{D}^{\mathrm{3}} +{D}^{\mathrm{2}} +\mathrm{3}{D}−\mathrm{5}}\left(\mathrm{5sin}\:\mathrm{2}{x}+\mathrm{10}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{7}\right) \\ $$$$=−\frac{\mathrm{1}}{{D}+\mathrm{9}}\mathrm{5sin}\:\mathrm{2}{x}−\frac{\mathrm{1}}{\mathrm{5}}\centerdot\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}\left({D}^{\mathrm{3}} +{D}^{\mathrm{2}} +\mathrm{3}{D}\right)}\left(\mathrm{10}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{7}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{17}}\left({D}−\mathrm{9}\right)\mathrm{sin}\:\mathrm{2}{x}−\frac{\mathrm{1}}{\mathrm{5}}\left\{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{5}}\left({D}^{\mathrm{3}} +{D}^{\mathrm{2}} +\mathrm{3}{D}\right)+\frac{\mathrm{1}}{\mathrm{25}}\left({D}^{\mathrm{3}} +{D}^{\mathrm{2}} +\mathrm{3}{D}\right)^{\mathrm{2}} +…\right\}\left(\mathrm{10}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{7}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{17}}\left(\mathrm{2cos}\:\mathrm{2}{x}−\mathrm{9sin}\:\mathrm{2}{x}\right)−\frac{\mathrm{1}}{\mathrm{5}}\left\{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{5}}{D}+\frac{\mathrm{14}}{\mathrm{25}}{D}^{\mathrm{2}} +…\right\}\left(\mathrm{10}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{7}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{17}}\left(\mathrm{2cos}\:\mathrm{2}{x}−\mathrm{9sin}\:\mathrm{2}{x}\right)+\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{4} \\ $$$${y}={C}_{\mathrm{1}} {e}^{{x}} +{e}^{−\mathrm{2}{x}} \left({C}_{\mathrm{2}} \mathrm{sin}\:\mathrm{2}{x}+{C}_{\mathrm{3}} \mathrm{cos}\:\mathrm{2}{x}\right)+\frac{\mathrm{1}}{\mathrm{17}}\left(\mathrm{2cos}\:\mathrm{2}{x}−\mathrm{9sin}\:\mathrm{2}{x}\right)+\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{4} \\ $$$$\left(\mathrm{7}\right){y}_{{p}} =\frac{\mathrm{1}}{{D}^{\mathrm{3}} +{D}}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4sin}\:{x}\right)=\frac{\mathrm{2}}{\mathrm{3}}\frac{\mathrm{1}}{{D}^{\mathrm{2}} +\mathrm{1}}{x}^{\mathrm{3}} −\frac{\mathrm{1}}{{D}^{\mathrm{2}} +\mathrm{1}}\mathrm{4cos}\:{x} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−{D}^{\mathrm{2}} −{D}^{\mathrm{4}} −…\right){x}^{\mathrm{3}} −{x}\frac{\mathrm{1}}{\left({D}^{\mathrm{2}} +\mathrm{1}\right)'}\mathrm{4cos}\:{x} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\left({x}^{\mathrm{3}} −\mathrm{6}{x}\right)−\mathrm{2}{x}\frac{\mathrm{1}}{{D}}\mathrm{cos}\:{x} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}{x}^{\mathrm{3}} −\mathrm{4}{x}−\mathrm{2}{x}\mathrm{sin}\:{x} \\ $$$${y}={C}_{\mathrm{1}} +{C}_{\mathrm{2}} \mathrm{sin}\:{x}+{C}_{\mathrm{3}} \mathrm{cos}\:{x}−\frac{\mathrm{2}}{\mathrm{3}}{x}^{\mathrm{3}} −\mathrm{4}{x}−\mathrm{2}{x}\mathrm{sin}\:{x} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *