Question Number 137111 by mnjuly1970 last updated on 29/Mar/21

Answered by Dwaipayan Shikari last updated on 29/Mar/21
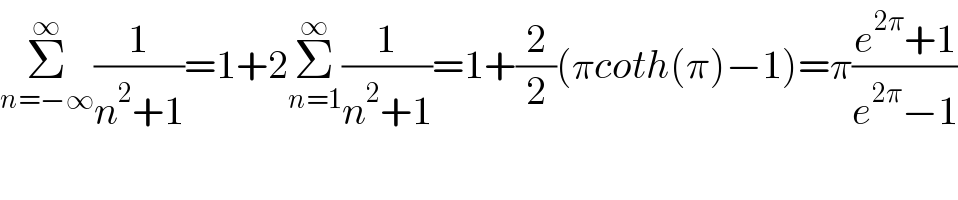
$$\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{1}}=\mathrm{1}+\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{1}}=\mathrm{1}+\frac{\mathrm{2}}{\mathrm{2}}\left(\pi{coth}\left(\pi\right)−\mathrm{1}\right)=\pi\frac{{e}^{\mathrm{2}\pi} +\mathrm{1}}{{e}^{\mathrm{2}\pi} −\mathrm{1}} \\ $$
