Question Number 137171 by mnjuly1970 last updated on 30/Mar/21
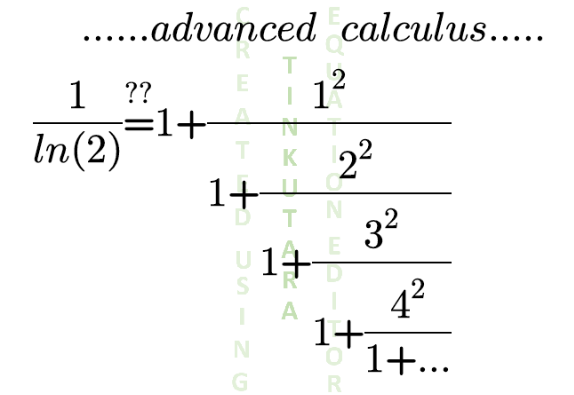
Answered by Dwaipayan Shikari last updated on 30/Mar/21
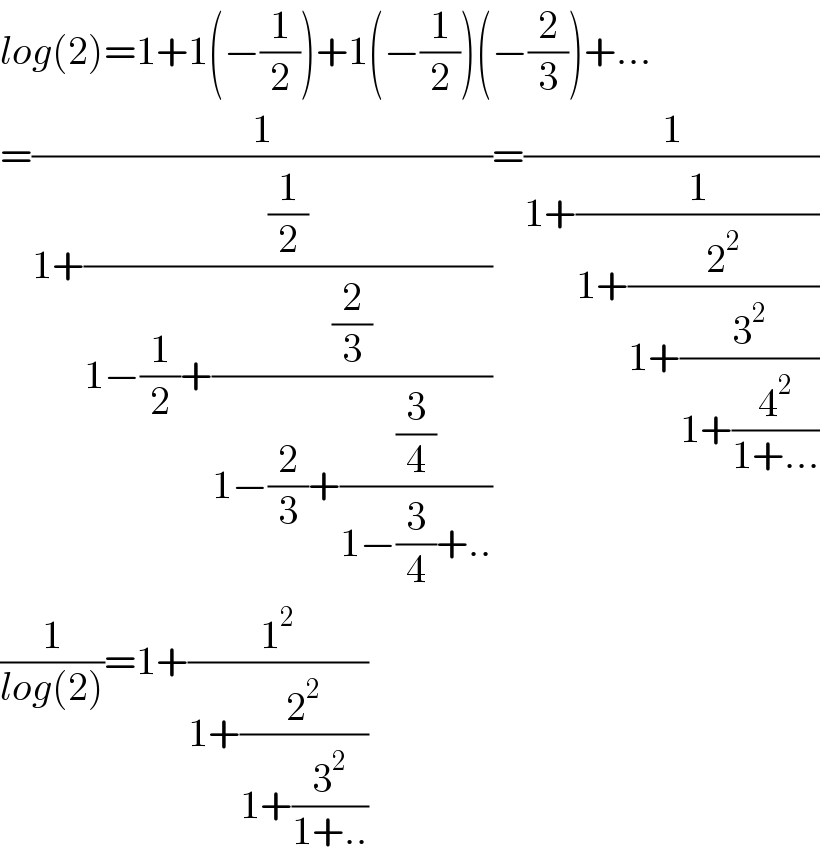
$${log}\left(\mathrm{2}\right)=\mathrm{1}+\mathrm{1}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{1}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(−\frac{\mathrm{2}}{\mathrm{3}}\right)+… \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\frac{\mathrm{2}}{\mathrm{3}}}{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}+\frac{\frac{\mathrm{3}}{\mathrm{4}}}{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}+..}}}}=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{1}+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{1}+\frac{\mathrm{4}^{\mathrm{2}} }{\mathrm{1}+…}}}}} \\ $$$$\frac{\mathrm{1}}{{log}\left(\mathrm{2}\right)}=\mathrm{1}+\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{1}+\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{1}+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{1}+..}}} \\ $$
Commented by Dwaipayan Shikari last updated on 30/Mar/21
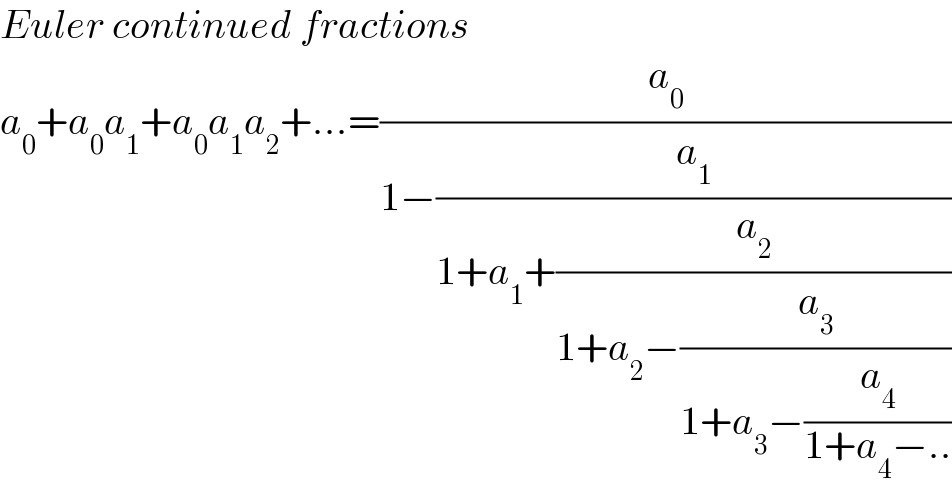
$${Euler}\:{continued}\:{fractions} \\ $$$${a}_{\mathrm{0}} +{a}_{\mathrm{0}} {a}_{\mathrm{1}} +{a}_{\mathrm{0}} {a}_{\mathrm{1}} {a}_{\mathrm{2}} +…=\frac{{a}_{\mathrm{0}} }{\mathrm{1}−\frac{{a}_{\mathrm{1}} }{\mathrm{1}+{a}_{\mathrm{1}} +\frac{{a}_{\mathrm{2}} }{\mathrm{1}+{a}_{\mathrm{2}} −\frac{{a}_{\mathrm{3}} }{\mathrm{1}+{a}_{\mathrm{3}} −\frac{{a}_{\mathrm{4}} }{\mathrm{1}+{a}_{\mathrm{4}} −..}}}}} \\ $$
Commented by mnjuly1970 last updated on 30/Mar/21
$${grateful}\:…\:{mr}\:{payan} \\ $$$${thanks}\:{alot}\:…. \\ $$
