Question Number 137206 by JulioCesar last updated on 31/Mar/21

Answered by bemath last updated on 31/Mar/21
![by parts { ((u=ln (((x−1)/(x+1))) du=(2/((x−1)(x+1)))dx)),((v = x)) :} I = x ln (((x−1)/(x+1)))−∫ ((2x)/((x−1)(x+1)))dx I=x ln (((x−1)/(x+1)))−[∫ (1/(x−1))dx+∫ (1/(x+1))dx ] I= x ln (((x−1)/(x+1)))−ln (x^2 −1) + C I = (x−1)ln (x−1)+(1−x)ln (x+1) + C](https://www.tinkutara.com/question/Q137207.png)
$$\mathrm{by}\:\mathrm{parts}\:\begin{cases}{\mathrm{u}=\mathrm{ln}\:\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right) \:\mathrm{du}=\frac{\mathrm{2}}{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{1}\right)}\mathrm{dx}}\\{\mathrm{v}\:=\:\mathrm{x}}\end{cases} \\ $$$$\mathrm{I}\:=\:\mathrm{x}\:\mathrm{ln}\:\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)−\int\:\frac{\mathrm{2x}}{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{1}\right)}\mathrm{dx} \\ $$$$\mathrm{I}=\mathrm{x}\:\mathrm{ln}\:\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)−\left[\int\:\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}\mathrm{dx}+\int\:\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\mathrm{dx}\:\right] \\ $$$$\mathrm{I}=\:\mathrm{x}\:\mathrm{ln}\:\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)−\mathrm{ln}\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\:+\:\mathrm{C} \\ $$$$\mathrm{I}\:=\:\left(\mathrm{x}−\mathrm{1}\right)\mathrm{ln}\:\left(\mathrm{x}−\mathrm{1}\right)+\left(\mathrm{1}−\mathrm{x}\right)\mathrm{ln}\:\left(\mathrm{x}+\mathrm{1}\right)\:+\:\mathrm{C} \\ $$
Answered by Ñï= last updated on 31/Mar/21
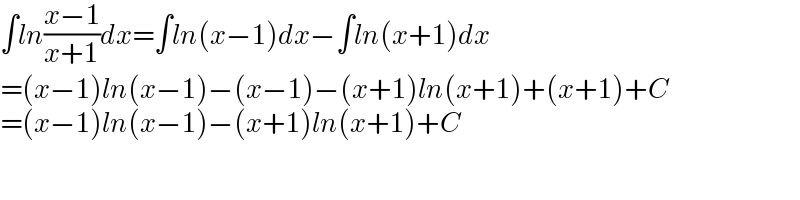
$$\int{ln}\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}{dx}=\int{ln}\left({x}−\mathrm{1}\right){dx}−\int{ln}\left({x}+\mathrm{1}\right){dx} \\ $$$$=\left({x}−\mathrm{1}\right){ln}\left({x}−\mathrm{1}\right)−\left({x}−\mathrm{1}\right)−\left({x}+\mathrm{1}\right){ln}\left({x}+\mathrm{1}\right)+\left({x}+\mathrm{1}\right)+{C} \\ $$$$=\left({x}−\mathrm{1}\right){ln}\left({x}−\mathrm{1}\right)−\left({x}+\mathrm{1}\right){ln}\left({x}+\mathrm{1}\right)+{C} \\ $$
