Question Number 137226 by SLVR last updated on 31/Mar/21

Answered by MJS_new last updated on 31/Mar/21
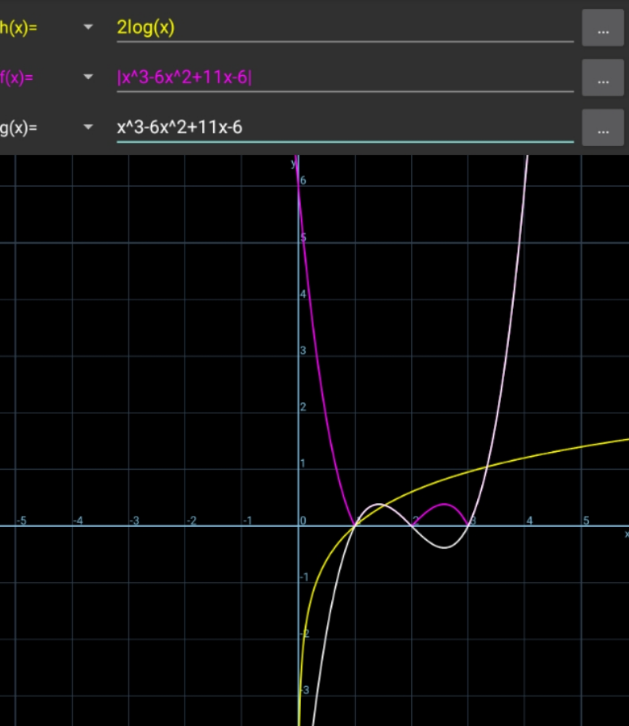
![f(x)=2ln x x^3 −6x^2 +11x−6=(x−1)(x−2)(x−3) the curves intersect at x=1 ∫_0 ^1 2ln x dx=[2xln x −2x]_0 ^1 =−2 ∫_0 ^1 (x^3 −6x^2 +11x−6)dx=[(x^4 /4)−2x^3 +((11x^2 )/2)−6x]_0 ^1 =−(9/4) area is −2+(9/4)=(1/4)](https://www.tinkutara.com/question/Q137242.png)
$${f}\left({x}\right)=\mathrm{2ln}\:{x} \\ $$$${x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{2}} +\mathrm{11}{x}−\mathrm{6}=\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right) \\ $$$$\mathrm{the}\:\mathrm{curves}\:\mathrm{intersect}\:\mathrm{at}\:{x}=\mathrm{1} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\mathrm{2ln}\:{x}\:{dx}=\left[\mathrm{2}{x}\mathrm{ln}\:{x}\:−\mathrm{2}{x}\right]_{\mathrm{0}} ^{\mathrm{1}} =−\mathrm{2} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left({x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{2}} +\mathrm{11}{x}−\mathrm{6}\right){dx}=\left[\frac{{x}^{\mathrm{4}} }{\mathrm{4}}−\mathrm{2}{x}^{\mathrm{3}} +\frac{\mathrm{11}{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{6}{x}\right]_{\mathrm{0}} ^{\mathrm{1}} =−\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\mathrm{area}\:\mathrm{is}\:−\mathrm{2}+\frac{\mathrm{9}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by SLVR last updated on 31/Mar/21
$${greart}\:{sir}..{thanks} \\ $$
Commented by mr W last updated on 31/Mar/21

$${the}\:{area}\:{bounded}\:{by}\:{y}={f}\left({x}\right)\:{and} \\ $$$${y}={x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{2}} +\mathrm{11}{x}−\mathrm{6}\:{is}\:\frac{\mathrm{1}}{\mathrm{4}}.\:{but}\:{the} \\ $$$${question}\:{asks}\:{the}\:{area}\:{bounded}\:{by} \\ $$$${y}={f}\left({x}\right)\:{and}\:{y}=\mid{x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{2}} +\mathrm{11}{x}−\mathrm{6}\mid, \\ $$$${which}\:{is}\:{then}\:\mathrm{2}+\frac{\mathrm{9}}{\mathrm{4}}=\frac{\mathrm{17}}{\mathrm{4}}. \\ $$$${so}\:{i}\:{think}\:{the}\:{question}\:{is}\:{wrong}. \\ $$
Commented by MJS_new last updated on 31/Mar/21

$$\mathrm{you}\:\mathrm{are}\:\mathrm{right} \\ $$
Commented by Dwaipayan Shikari last updated on 31/Mar/21