Question Number 137359 by rexford last updated on 01/Apr/21

Answered by Ar Brandon last updated on 01/Apr/21
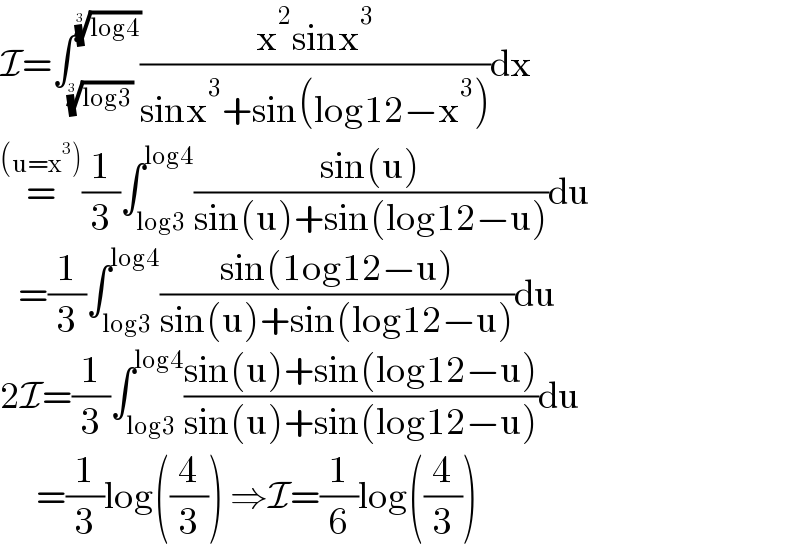
$$\mathcal{I}=\int_{\sqrt[{\mathrm{3}}]{\mathrm{log3}}} ^{\sqrt[{\mathrm{3}}]{\mathrm{log4}}} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{sinx}^{\mathrm{3}} }{\mathrm{sinx}^{\mathrm{3}} +\mathrm{sin}\left(\mathrm{log12}−\mathrm{x}^{\mathrm{3}} \right)}\mathrm{dx} \\ $$$$\overset{\left(\mathrm{u}=\mathrm{x}^{\mathrm{3}} \right)} {=}\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{log3}} ^{\mathrm{log4}} \frac{\mathrm{sin}\left(\mathrm{u}\right)}{\mathrm{sin}\left(\mathrm{u}\right)+\mathrm{sin}\left(\mathrm{log12}−\mathrm{u}\right)}\mathrm{du} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{log3}} ^{\mathrm{log4}} \frac{\mathrm{sin}\left(\mathrm{1og12}−\mathrm{u}\right)}{\mathrm{sin}\left(\mathrm{u}\right)+\mathrm{sin}\left(\mathrm{log12}−\mathrm{u}\right)}\mathrm{du} \\ $$$$\mathrm{2}\mathcal{I}=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{log3}} ^{\mathrm{log4}} \frac{\mathrm{sin}\left(\mathrm{u}\right)+\mathrm{sin}\left(\mathrm{log12}−\mathrm{u}\right)}{\mathrm{sin}\left(\mathrm{u}\right)+\mathrm{sin}\left(\mathrm{log12}−\mathrm{u}\right)}\mathrm{du} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{log}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)\:\Rightarrow\mathcal{I}=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{log}\left(\frac{\mathrm{4}}{\mathrm{3}}\right) \\ $$
