Question Number 137379 by oooooooo last updated on 02/Apr/21
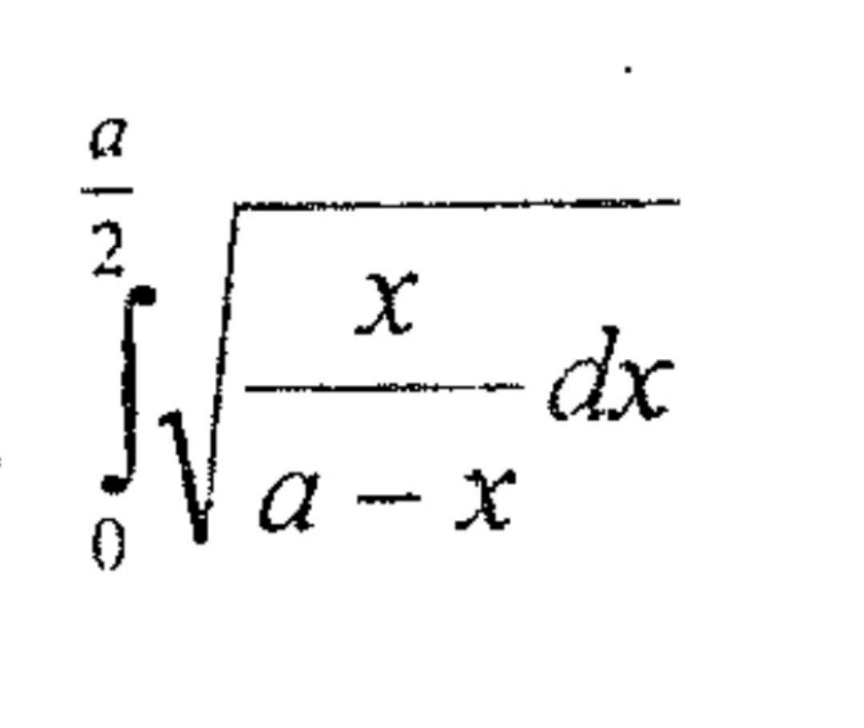
Answered by Ar Brandon last updated on 02/Apr/21
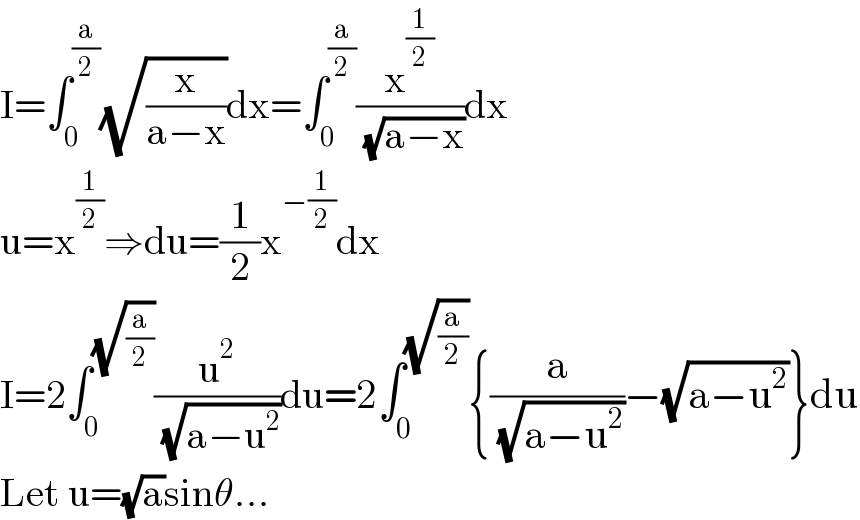
$$\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\mathrm{a}}{\mathrm{2}}} \sqrt{\frac{\mathrm{x}}{\mathrm{a}−\mathrm{x}}}\mathrm{dx}=\int_{\mathrm{0}} ^{\frac{\mathrm{a}}{\mathrm{2}}} \frac{\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\:\sqrt{\mathrm{a}−\mathrm{x}}}\mathrm{dx} \\ $$$$\mathrm{u}=\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} \Rightarrow\mathrm{du}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{dx} \\ $$$$\mathrm{I}=\mathrm{2}\int_{\mathrm{0}} ^{\sqrt{\frac{\mathrm{a}}{\mathrm{2}}}} \frac{\mathrm{u}^{\mathrm{2}} }{\:\sqrt{\mathrm{a}−\mathrm{u}^{\mathrm{2}} }}\mathrm{du}=\mathrm{2}\int_{\mathrm{0}} ^{\sqrt{\frac{\mathrm{a}}{\mathrm{2}}}} \left\{\frac{\mathrm{a}}{\:\sqrt{\mathrm{a}−\mathrm{u}^{\mathrm{2}} }}−\sqrt{\mathrm{a}−\mathrm{u}^{\mathrm{2}} }\right\}\mathrm{du} \\ $$$$\mathrm{Let}\:\mathrm{u}=\sqrt{\mathrm{a}}\mathrm{sin}\theta… \\ $$
Commented by mathmax by abdo last updated on 02/Apr/21
![Φ=∫_0 ^(a/2) (√(x/(a−x)))dx changement (√(x/(a−x)))=t give (x/(a−x))=t^2 ⇒ x=at^2 −t^2 x ⇒(1+t^2 )x=at^2 ⇒x=((at^2 )/(1+t^2 )) ⇒(dx/dt)=((2at(1+t^2 )−at^2 (2t))/((1+t^2 )^2 )) =((2at)/((1+t^2 )^2 )) ⇒Φ = ∫_0 ^1 t×((2at)/((1+t^2 )^2 ))dt =2a ∫_0 ^1 (t^2 /((1+t^2 )^2 ))dt =2a∫_0 ^1 ((1+t^2 −1)/((1+t^2 )^2 ))dt =2a ∫_0 ^1 (dt/(1+t^2 )) −2a ∫_0 ^1 (dt/((1+t^2 )^2 )) we have ∫_0 ^1 (dt/(1+t^2 ))=[arctant]_0 ^1 =(π/4) ∫_0 ^1 (dt/((1+t^2 )^2 )) =_(t=tanu) ∫_0 ^(π/4) ((1+tan^2 u)/((1+tan^2 u)^2 ))du =∫_0 ^(π/4) (du/(1+tan^2 u)) =∫_0 ^(π/4) cos^2 u du =(1/2)∫_0 ^(π/4) (1+cos(2u))du =(π/8) +(1/4)[sin(2u)]_0 ^(π/4) =(π/8)+(1/4) ⇒ Φ= ((πa)/2)−2a((π/8)+(1/4)) =((πa)/2)−((πa)/4) +(a/2) =((πa)/4)+(a/2) =((1/2)+(π/4))a](https://www.tinkutara.com/question/Q137409.png)
$$\Phi=\int_{\mathrm{0}} ^{\frac{\mathrm{a}}{\mathrm{2}}} \sqrt{\frac{\mathrm{x}}{\mathrm{a}−\mathrm{x}}}\mathrm{dx}\:\:\:\mathrm{changement}\:\sqrt{\frac{\mathrm{x}}{\mathrm{a}−\mathrm{x}}}=\mathrm{t}\:\:\mathrm{give}\:\frac{\mathrm{x}}{\mathrm{a}−\mathrm{x}}=\mathrm{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{x}=\mathrm{at}^{\mathrm{2}} −\mathrm{t}^{\mathrm{2}} \mathrm{x}\:\Rightarrow\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\mathrm{x}=\mathrm{at}^{\mathrm{2}} \:\Rightarrow\mathrm{x}=\frac{\mathrm{at}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:\Rightarrow\frac{\mathrm{dx}}{\mathrm{dt}}=\frac{\mathrm{2at}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)−\mathrm{at}^{\mathrm{2}} \left(\mathrm{2t}\right)}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2at}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\Rightarrow\Phi\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\mathrm{t}×\frac{\mathrm{2at}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\mathrm{2a}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{t}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}\:=\mathrm{2a}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\mathrm{2a}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:−\mathrm{2a}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }=\left[\mathrm{arctant}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\pi}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=_{\mathrm{t}=\mathrm{tanu}} \:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{u}}{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{u}\right)^{\mathrm{2}} }\mathrm{du}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{du}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{u}} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{cos}^{\mathrm{2}} \mathrm{u}\:\mathrm{du}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2u}\right)\right)\mathrm{du}\:=\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{sin}\left(\mathrm{2u}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\frac{\pi}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\:\Phi=\:\frac{\pi\mathrm{a}}{\mathrm{2}}−\mathrm{2a}\left(\frac{\pi}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{4}}\right)\:=\frac{\pi\mathrm{a}}{\mathrm{2}}−\frac{\pi\mathrm{a}}{\mathrm{4}}\:+\frac{\mathrm{a}}{\mathrm{2}} \\ $$$$=\frac{\pi\mathrm{a}}{\mathrm{4}}+\frac{\mathrm{a}}{\mathrm{2}}\:=\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\mathrm{a} \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 03/Apr/21
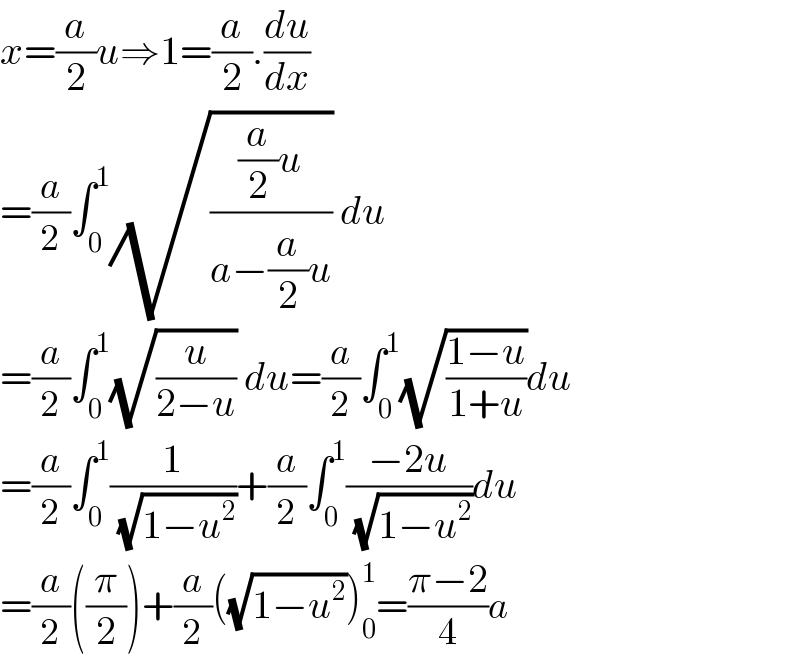
$${x}=\frac{{a}}{\mathrm{2}}{u}\Rightarrow\mathrm{1}=\frac{{a}}{\mathrm{2}}.\frac{{du}}{{dx}} \\ $$$$=\frac{{a}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\frac{\frac{{a}}{\mathrm{2}}{u}}{{a}−\frac{{a}}{\mathrm{2}}{u}}}\:{du} \\ $$$$=\frac{{a}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\frac{{u}}{\mathrm{2}−{u}}}\:{du}=\frac{{a}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{1}−{u}}{\mathrm{1}+{u}}}{du} \\ $$$$=\frac{{a}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}+\frac{{a}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−\mathrm{2}{u}}{\:\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}{du} \\ $$$$=\frac{{a}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}\right)+\frac{{a}}{\mathrm{2}}\left(\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }\right)_{\mathrm{0}} ^{\mathrm{1}} =\frac{\pi−\mathrm{2}}{\mathrm{4}}{a} \\ $$
Answered by MJS_new last updated on 03/Apr/21
![∫(√(x/(a−x)))dx= [t=(√(x/(a−x))) → dx=((2at)/((t^2 +1)^2 ))dt] =2a∫(t^2 /((t^2 +1)^2 ))dt=2a∫(dt/(t^2 +1))−2a∫(dt/((t^2 +1)))= =aarctan t −((at)/(t^2 +1))= =aarctan (√(x/(a−x))) −(√(x(a−x)))+C ⇒ answer is (((π−2)a)/4)](https://www.tinkutara.com/question/Q137452.png)
$$\int\sqrt{\frac{{x}}{{a}−{x}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\frac{{x}}{{a}−{x}}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{at}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt}\right] \\ $$$$=\mathrm{2}{a}\int\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt}=\mathrm{2}{a}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}−\mathrm{2}{a}\int\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)}= \\ $$$$={a}\mathrm{arctan}\:{t}\:−\frac{{at}}{{t}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$={a}\mathrm{arctan}\:\sqrt{\frac{{x}}{{a}−{x}}}\:−\sqrt{{x}\left({a}−{x}\right)}+{C} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\left(\pi−\mathrm{2}\right){a}}{\mathrm{4}} \\ $$
