Question Number 137467 by SOMEDAVONG last updated on 03/Apr/21
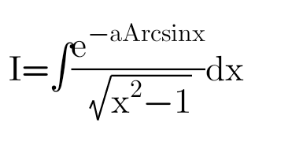
Answered by Ñï= last updated on 03/Apr/21
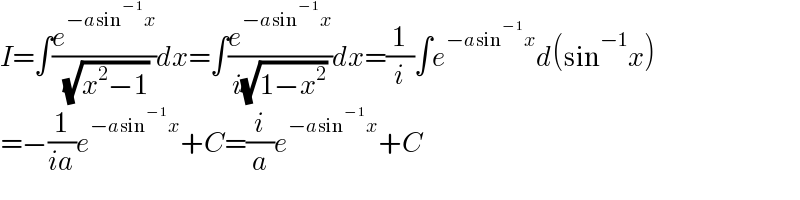
$${I}=\int\frac{{e}^{−{a}\mathrm{sin}^{−\mathrm{1}} {x}} }{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{dx}=\int\frac{{e}^{−{a}\mathrm{sin}^{−\mathrm{1}} {x}} }{{i}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}=\frac{\mathrm{1}}{{i}}\int{e}^{−{a}\mathrm{sin}^{−\mathrm{1}} {x}} {d}\left(\mathrm{sin}^{−\mathrm{1}} {x}\right) \\ $$$$=−\frac{\mathrm{1}}{{ia}}{e}^{−{a}\mathrm{sin}^{−\mathrm{1}} {x}} +{C}=\frac{{i}}{{a}}{e}^{−{a}\mathrm{sin}^{−\mathrm{1}} {x}} +{C} \\ $$
