Question-137618

Question Number 137618 by I want to learn more last updated on 04/Apr/21

Commented by I want to learn more last updated on 04/Apr/21

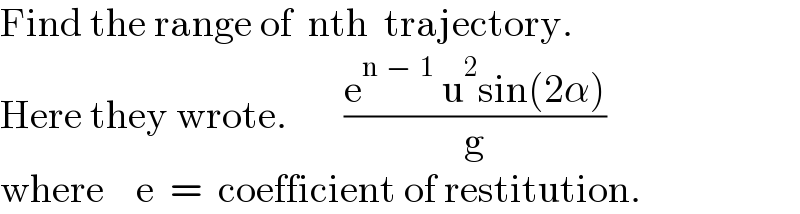
Find the range of nth trajectory. Here they wrote. ((e^(n − 1) u^2 sin(2α))/g) where e = coefficient of restitution.

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{range}\:\mathrm{of}\:\:\mathrm{nth}\:\:\mathrm{trajectory}. \\ $$$$\mathrm{Here}\:\mathrm{they}\:\mathrm{wrote}.\:\:\:\:\:\:\:\frac{\mathrm{e}^{\mathrm{n}\:\:−\:\:\mathrm{1}} \:\mathrm{u}^{\mathrm{2}} \mathrm{sin}\left(\mathrm{2}\alpha\right)}{\mathrm{g}} \\ $$$$\mathrm{where}\:\:\:\:\mathrm{e}\:\:=\:\:\mathrm{coefficient}\:\mathrm{of}\:\mathrm{restitution}. \\ $$

Commented by Tawa11 last updated on 14/Sep/21

$$\mathrm{nice} \\ $$

Answered by mr W last updated on 04/Apr/21

Commented by mr W last updated on 04/Apr/21

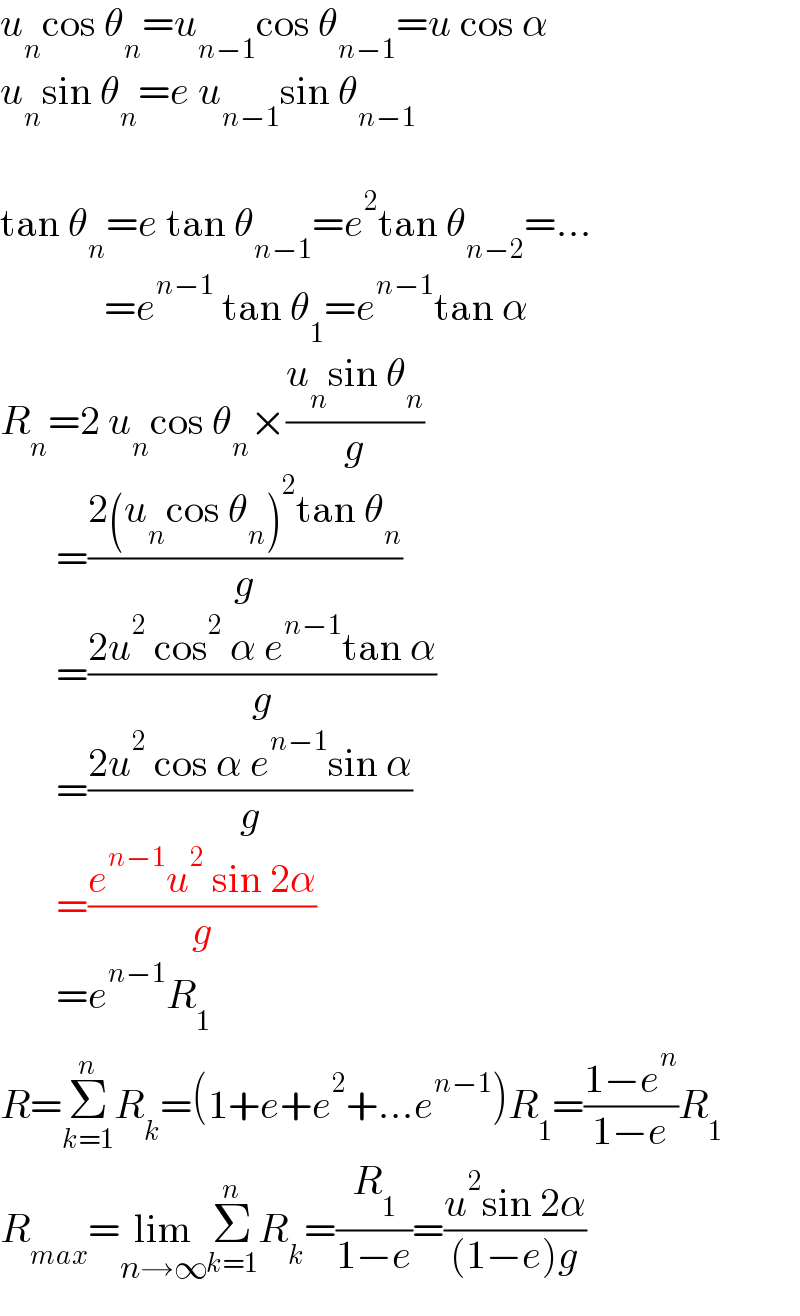
u_n cos θ_n =u_(n−1) cos θ_(n−1) =u cos α u_n sin θ_n =e u_(n−1) sin θ_(n−1) tan θ_n =e tan θ_(n−1) =e^2 tan θ_(n−2) =... =e^(n−1) tan θ_1 =e^(n−1) tan α R_n =2 u_n cos θ_n ×((u_n sin θ_n )/g) =((2(u_n cos θ_n )^2 tan θ_n )/g) =((2u^2 cos^2 α e^(n−1) tan α)/g) =((2u^2 cos α e^(n−1) sin α)/g) =((e^(n−1) u^2 sin 2α)/g) =e^(n−1) R_1 R=Σ_(k=1) ^n R_k =(1+e+e^2 +...e^(n−1) )R_1 =((1−e^n )/(1−e))R_1 R_(max) =lim_(n→∞) Σ_(k=1) ^n R_k =(R_1 /(1−e))=((u^2 sin 2α)/((1−e)g))

$${u}_{{n}} \mathrm{cos}\:\theta_{{n}} ={u}_{{n}−\mathrm{1}} \mathrm{cos}\:\theta_{{n}−\mathrm{1}} ={u}\:\mathrm{cos}\:\alpha \\ $$$${u}_{{n}} \mathrm{sin}\:\theta_{{n}} ={e}\:{u}_{{n}−\mathrm{1}} \mathrm{sin}\:\theta_{{n}−\mathrm{1}} \\ $$$$ \\ $$$$\mathrm{tan}\:\theta_{{n}} ={e}\:\mathrm{tan}\:\theta_{{n}−\mathrm{1}} ={e}^{\mathrm{2}} \mathrm{tan}\:\theta_{{n}−\mathrm{2}} =… \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:={e}^{{n}−\mathrm{1}} \:\mathrm{tan}\:\theta_{\mathrm{1}} ={e}^{{n}−\mathrm{1}} \mathrm{tan}\:\alpha \\ $$$${R}_{{n}} =\mathrm{2}\:{u}_{{n}} \mathrm{cos}\:\theta_{{n}} ×\frac{{u}_{{n}} \mathrm{sin}\:\theta_{{n}} }{{g}} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{2}\left({u}_{{n}} \mathrm{cos}\:\theta_{{n}} \right)^{\mathrm{2}} \mathrm{tan}\:\theta_{{n}} }{{g}} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{2}{u}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\alpha\:{e}^{{n}−\mathrm{1}} \mathrm{tan}\:\alpha}{{g}} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{2}{u}^{\mathrm{2}} \:\mathrm{cos}\:\alpha\:{e}^{{n}−\mathrm{1}} \mathrm{sin}\:\alpha}{{g}} \\ $$$$\:\:\:\:\:\:\:=\frac{{e}^{{n}−\mathrm{1}} {u}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{2}\alpha}{{g}} \\ $$$$\:\:\:\:\:\:\:={e}^{{n}−\mathrm{1}} {R}_{\mathrm{1}} \\ $$$${R}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{R}_{{k}} =\left(\mathrm{1}+{e}+{e}^{\mathrm{2}} +…{e}^{{n}−\mathrm{1}} \right){R}_{\mathrm{1}} =\frac{\mathrm{1}−{e}^{{n}} }{\mathrm{1}−{e}}{R}_{\mathrm{1}} \\ $$$${R}_{{max}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{R}_{{k}} =\frac{{R}_{\mathrm{1}} }{\mathrm{1}−{e}}=\frac{{u}^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\alpha}{\left(\mathrm{1}−{e}\right){g}} \\ $$

Commented by I want to learn more last updated on 04/Apr/21

Wow, i really appreciate sir. God bless you.

$$\mathrm{Wow},\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply