Question Number 137698 by JulioCesar last updated on 05/Apr/21

Commented by peter frank last updated on 06/Apr/21
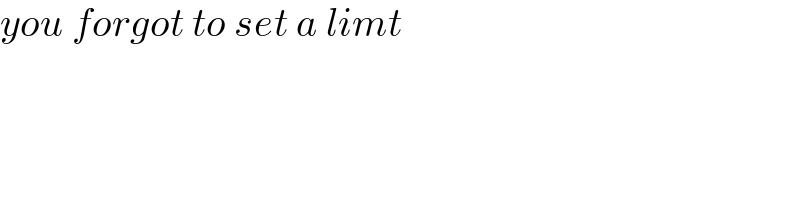
$${you}\:{forgot}\:{to}\:{set}\:{a}\:{limt} \\ $$
Answered by peter frank last updated on 06/Apr/21
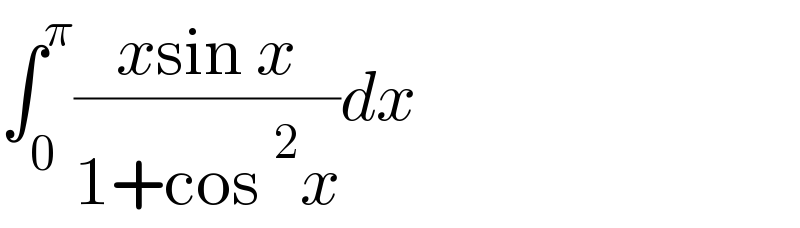
$$\int_{\mathrm{0}} ^{\pi} \frac{{x}\mathrm{sin}\:{x}}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} {x}}{dx} \\ $$
Commented by SEKRET last updated on 07/Apr/21
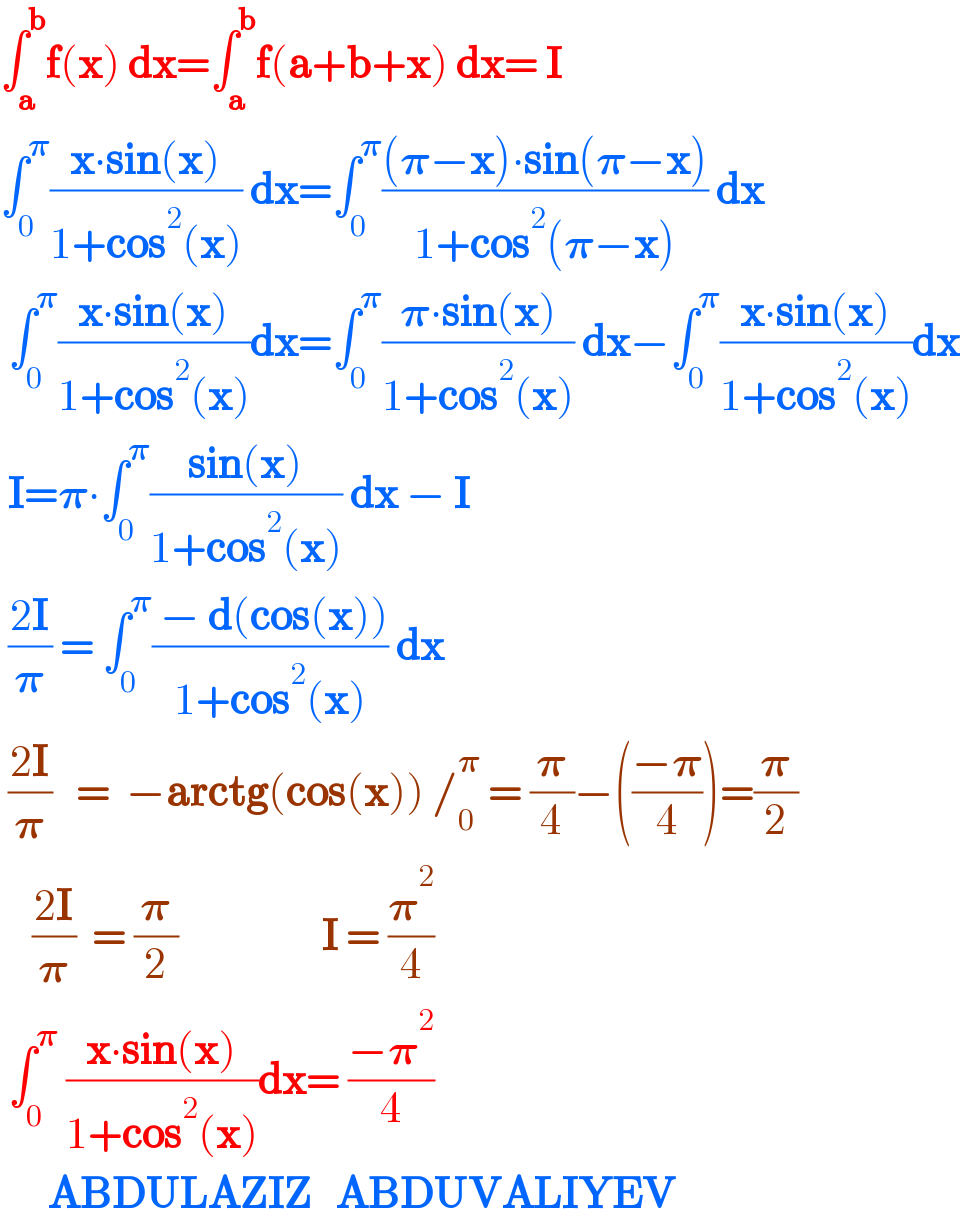
$$\int_{\boldsymbol{\mathrm{a}}} ^{\boldsymbol{\mathrm{b}}} \boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)\:\boldsymbol{\mathrm{dx}}=\int_{\boldsymbol{\mathrm{a}}} ^{\boldsymbol{\mathrm{b}}} \boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{x}}\right)\:\boldsymbol{\mathrm{dx}}=\:\boldsymbol{\mathrm{I}} \\ $$$$\int_{\mathrm{0}} ^{\boldsymbol{\pi}} \frac{\boldsymbol{\mathrm{x}}\centerdot\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)}{\mathrm{1}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}\right)}\:\boldsymbol{\mathrm{dx}}=\int_{\mathrm{0}} ^{\boldsymbol{\pi}} \frac{\left(\boldsymbol{\pi}−\boldsymbol{\mathrm{x}}\right)\centerdot\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\pi}−\boldsymbol{\mathrm{x}}\right)}{\mathrm{1}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \left(\boldsymbol{\pi}−\boldsymbol{\mathrm{x}}\right)}\:\boldsymbol{\mathrm{dx}} \\ $$$$\:\int_{\mathrm{0}} ^{\boldsymbol{\pi}} \frac{\boldsymbol{\mathrm{x}}\centerdot\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)}{\mathrm{1}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}\right)}\boldsymbol{\mathrm{dx}}=\int_{\mathrm{0}} ^{\boldsymbol{\pi}} \frac{\boldsymbol{\pi}\centerdot\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)}{\mathrm{1}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}\right)}\:\boldsymbol{\mathrm{dx}}−\int_{\mathrm{0}} ^{\boldsymbol{\pi}} \frac{\boldsymbol{\mathrm{x}}\centerdot\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)}{\mathrm{1}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}\right)}\boldsymbol{\mathrm{dx}} \\ $$$$\:\boldsymbol{\mathrm{I}}=\boldsymbol{\pi}\centerdot\int_{\mathrm{0}} ^{\boldsymbol{\pi}} \frac{\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)}{\mathrm{1}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}\right)}\:\boldsymbol{\mathrm{dx}}\:−\:\boldsymbol{\mathrm{I}} \\ $$$$\:\frac{\mathrm{2}\boldsymbol{\mathrm{I}}}{\boldsymbol{\pi}}\:=\:\int_{\mathrm{0}} ^{\boldsymbol{\pi}} \frac{\:−\:\boldsymbol{\mathrm{d}}\left(\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right)\right)}{\mathrm{1}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}\right)}\:\boldsymbol{\mathrm{dx}} \\ $$$$\:\frac{\mathrm{2}\boldsymbol{\mathrm{I}}}{\boldsymbol{\pi}}\:\:\:=\:\:−\boldsymbol{\mathrm{arctg}}\left(\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right)\right)\:/_{\mathrm{0}} ^{\boldsymbol{\pi}} \:=\:\frac{\boldsymbol{\pi}}{\mathrm{4}}−\left(\frac{−\boldsymbol{\pi}}{\mathrm{4}}\right)=\frac{\boldsymbol{\pi}}{\mathrm{2}} \\ $$$$\:\:\:\:\frac{\mathrm{2}\boldsymbol{\mathrm{I}}}{\boldsymbol{\pi}}\:\:=\:\frac{\boldsymbol{\pi}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{I}}\:=\:\frac{\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\:\int_{\mathrm{0}} ^{\boldsymbol{\pi}} \:\frac{\boldsymbol{\mathrm{x}}\centerdot\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)}{\mathrm{1}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}\right)}\boldsymbol{\mathrm{dx}}=\:\frac{−\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\boldsymbol{\mathrm{ABDULAZIZ}}\:\:\:\boldsymbol{\mathrm{ABDUVALIYEV}} \\ $$
