Menu Close

Question-137772

Tinku Tara 0 Comments
Pin




Question Number 137772 by peter frank last updated on 06/Apr/21
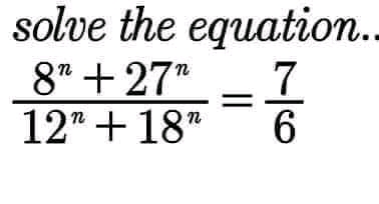
Answered by bemath last updated on 06/Apr/21
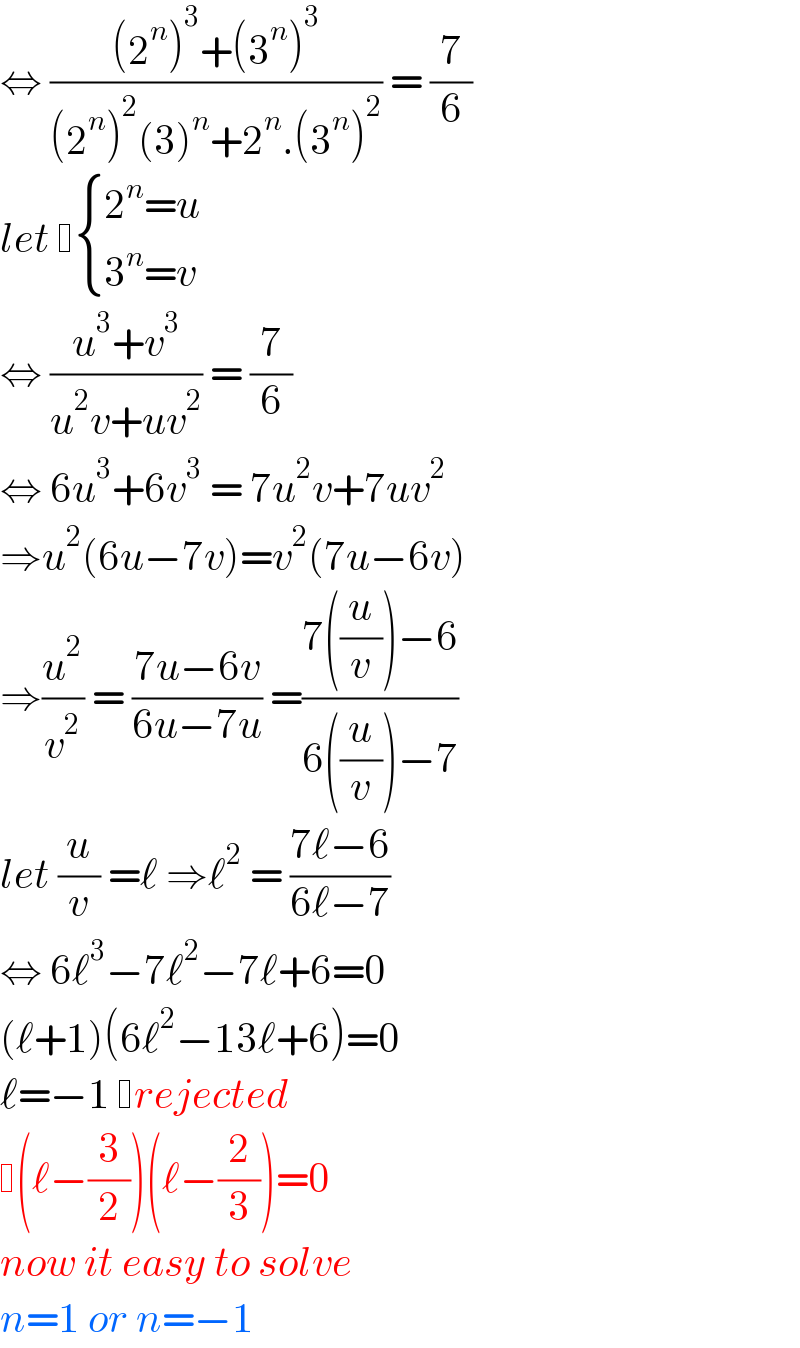
⇔ (((2^n )^3 +(3^n )^3 )/((2^n )^2 (3)^n +2^n .(3^n )^2 )) = (7/6) let { ((2^n =u)),((3^n =v)) :} ⇔ ((u^3 +v^3 )/(u^2 v+uv^2 )) = (7/6) ⇔ 6u^3 +6v^3 = 7u^2 v+7uv^2 ⇒u^2 (6u−7v)=v^2 (7u−6v) ⇒(u^2 /v^2 ) = ((7u−6v)/(6u−7u)) =((7((u/v))−6)/(6((u/v))−7)) let (u/v) =ℓ ⇒ℓ^2 = ((7ℓ−6)/(6ℓ−7)) ⇔ 6ℓ^3 −7ℓ^2 −7ℓ+6=0 (ℓ+1)(6ℓ^2 −13ℓ+6)=0 ℓ=−1 rejected (ℓ−(3/2))(ℓ−(2/3))=0 now it easy to solve n=1 or n=−1
$$\Leftrightarrow\:\frac{\left(\mathrm{2}^{{n}} \right)^{\mathrm{3}} +\left(\mathrm{3}^{{n}} \right)^{\mathrm{3}} }{\left(\mathrm{2}^{{n}} \right)^{\mathrm{2}} \left(\mathrm{3}\right)^{{n}} +\mathrm{2}^{{n}} .\left(\mathrm{3}^{{n}} \right)^{\mathrm{2}} }\:=\:\frac{\mathrm{7}}{\mathrm{6}} \\ $$$${let}\: \begin{cases}{\mathrm{2}^{{n}} ={u}}\\{\mathrm{3}^{{n}} ={v}}\end{cases} \\ $$$$\Leftrightarrow\:\frac{{u}^{\mathrm{3}} +{v}^{\mathrm{3}} }{{u}^{\mathrm{2}} {v}+{uv}^{\mathrm{2}} }\:=\:\frac{\mathrm{7}}{\mathrm{6}}\: \\ $$$$\Leftrightarrow\:\mathrm{6}{u}^{\mathrm{3}} +\mathrm{6}{v}^{\mathrm{3}} \:=\:\mathrm{7}{u}^{\mathrm{2}} {v}+\mathrm{7}{uv}^{\mathrm{2}} \\ $$$$\Rightarrow{u}^{\mathrm{2}} \left(\mathrm{6}{u}−\mathrm{7}{v}\right)={v}^{\mathrm{2}} \left(\mathrm{7}{u}−\mathrm{6}{v}\right) \\ $$$$\Rightarrow\frac{{u}^{\mathrm{2}} }{{v}^{\mathrm{2}} }\:=\:\frac{\mathrm{7}{u}−\mathrm{6}{v}}{\mathrm{6}{u}−\mathrm{7}{u}}\:=\frac{\mathrm{7}\left(\frac{{u}}{{v}}\right)−\mathrm{6}}{\mathrm{6}\left(\frac{{u}}{{v}}\right)−\mathrm{7}} \\ $$$${let}\:\frac{{u}}{{v}}\:=\ell\:\Rightarrow\ell^{\mathrm{2}} \:=\:\frac{\mathrm{7}\ell−\mathrm{6}}{\mathrm{6}\ell−\mathrm{7}} \\ $$$$\Leftrightarrow\:\mathrm{6}\ell^{\mathrm{3}} −\mathrm{7}\ell^{\mathrm{2}} −\mathrm{7}\ell+\mathrm{6}=\mathrm{0} \\ $$$$\left(\ell+\mathrm{1}\right)\left(\mathrm{6}\ell^{\mathrm{2}} −\mathrm{13}\ell+\mathrm{6}\right)=\mathrm{0} \\ $$$$\ell=−\mathrm{1}\: {rejected} \\ $$$$ \left(\ell−\frac{\mathrm{3}}{\mathrm{2}}\right)\left(\ell−\frac{\mathrm{2}}{\mathrm{3}}\right)=\mathrm{0} \\ $$$${now}\:{it}\:{easy}\:{to}\:{solve} \\ $$$${n}=\mathrm{1}\:{or}\:{n}=−\mathrm{1} \\ $$
Answered by Rasheed.Sindhi last updated on 07/Apr/21
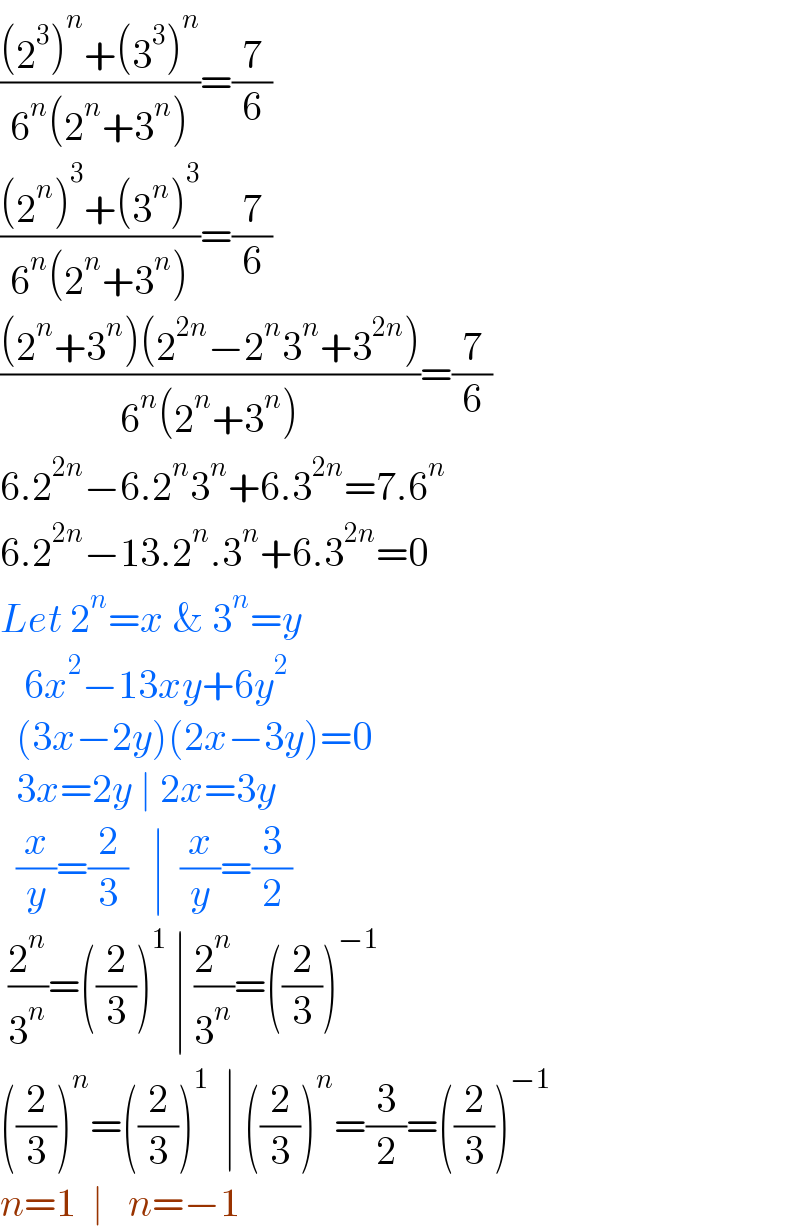
(((2^3 )^n +(3^3 )^n )/(6^n (2^n +3^n )))=(7/6) (((2^n )^3 +(3^n )^3 )/(6^n (2^n +3^n )))=(7/6) (((2^n +3^n )(2^(2n) −2^n 3^n +3^(2n) ))/(6^n (2^n +3^n )))=(7/6) 6.2^(2n) −6.2^n 3^n +6.3^(2n) =7.6^n 6.2^(2n) −13.2^n .3^n +6.3^(2n) =0 Let 2^n =x & 3^n =y 6x^2 −13xy+6y^2 (3x−2y)(2x−3y)=0 3x=2y ∣ 2x=3y (x/y)=(2/3) ∣ (x/y)=(3/2) (2^n /3^n )=((2/3))^1 ∣ (2^n /3^n )=((2/3))^(−1) ((2/3))^n =((2/3))^1 ∣ ((2/3))^n =(3/2)=((2/3))^(−1) n=1 ∣ n=−1
$$\frac{\left(\mathrm{2}^{\mathrm{3}} \right)^{{n}} +\left(\mathrm{3}^{\mathrm{3}} \right)^{{n}} }{\mathrm{6}^{{n}} \left(\mathrm{2}^{{n}} +\mathrm{3}^{{n}} \right)}=\frac{\mathrm{7}}{\mathrm{6}} \\ $$$$\frac{\left(\mathrm{2}^{{n}} \right)^{\mathrm{3}} +\left(\mathrm{3}^{{n}} \right)^{\mathrm{3}} }{\mathrm{6}^{{n}} \left(\mathrm{2}^{{n}} +\mathrm{3}^{{n}} \right)}=\frac{\mathrm{7}}{\mathrm{6}} \\ $$$$\frac{\left(\mathrm{2}^{{n}} +\mathrm{3}^{{n}} \right)\left(\mathrm{2}^{\mathrm{2}{n}} −\mathrm{2}^{{n}} \mathrm{3}^{{n}} +\mathrm{3}^{\mathrm{2}{n}} \right)}{\mathrm{6}^{{n}} \left(\mathrm{2}^{{n}} +\mathrm{3}^{{n}} \right)}=\frac{\mathrm{7}}{\mathrm{6}} \\ $$$$\mathrm{6}.\mathrm{2}^{\mathrm{2}{n}} −\mathrm{6}.\mathrm{2}^{{n}} \mathrm{3}^{{n}} +\mathrm{6}.\mathrm{3}^{\mathrm{2}{n}} =\mathrm{7}.\mathrm{6}^{{n}} \\ $$$$\mathrm{6}.\mathrm{2}^{\mathrm{2}{n}} −\mathrm{13}.\mathrm{2}^{{n}} .\mathrm{3}^{{n}} +\mathrm{6}.\mathrm{3}^{\mathrm{2}{n}} =\mathrm{0} \\ $$$${Let}\:\mathrm{2}^{{n}} ={x}\:\&\:\mathrm{3}^{{n}} ={y} \\ $$$$\:\:\:\mathrm{6}{x}^{\mathrm{2}} −\mathrm{13}{xy}+\mathrm{6}{y}^{\mathrm{2}} \\ $$$$\:\:\left(\mathrm{3}{x}−\mathrm{2}{y}\right)\left(\mathrm{2}{x}−\mathrm{3}{y}\right)=\mathrm{0} \\ $$$$\:\:\mathrm{3}{x}=\mathrm{2}{y}\:\mid\:\mathrm{2}{x}=\mathrm{3}{y} \\ $$$$\:\:\frac{{x}}{{y}}=\frac{\mathrm{2}}{\mathrm{3}}\:\:\:\mid\:\:\frac{{x}}{{y}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\frac{\mathrm{2}^{{n}} }{\mathrm{3}^{{n}} }=\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{1}} \:\mid\:\frac{\mathrm{2}^{{n}} }{\mathrm{3}^{{n}} }=\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{−\mathrm{1}} \\ $$$$\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}} =\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{1}} \:\:\mid\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}} =\frac{\mathrm{3}}{\mathrm{2}}=\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{−\mathrm{1}} \\ $$$${n}=\mathrm{1}\:\:\mid\:\:\:{n}=−\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *