Question Number 138003 by benjo_mathlover last updated on 09/Apr/21

Answered by EDWIN88 last updated on 09/Apr/21
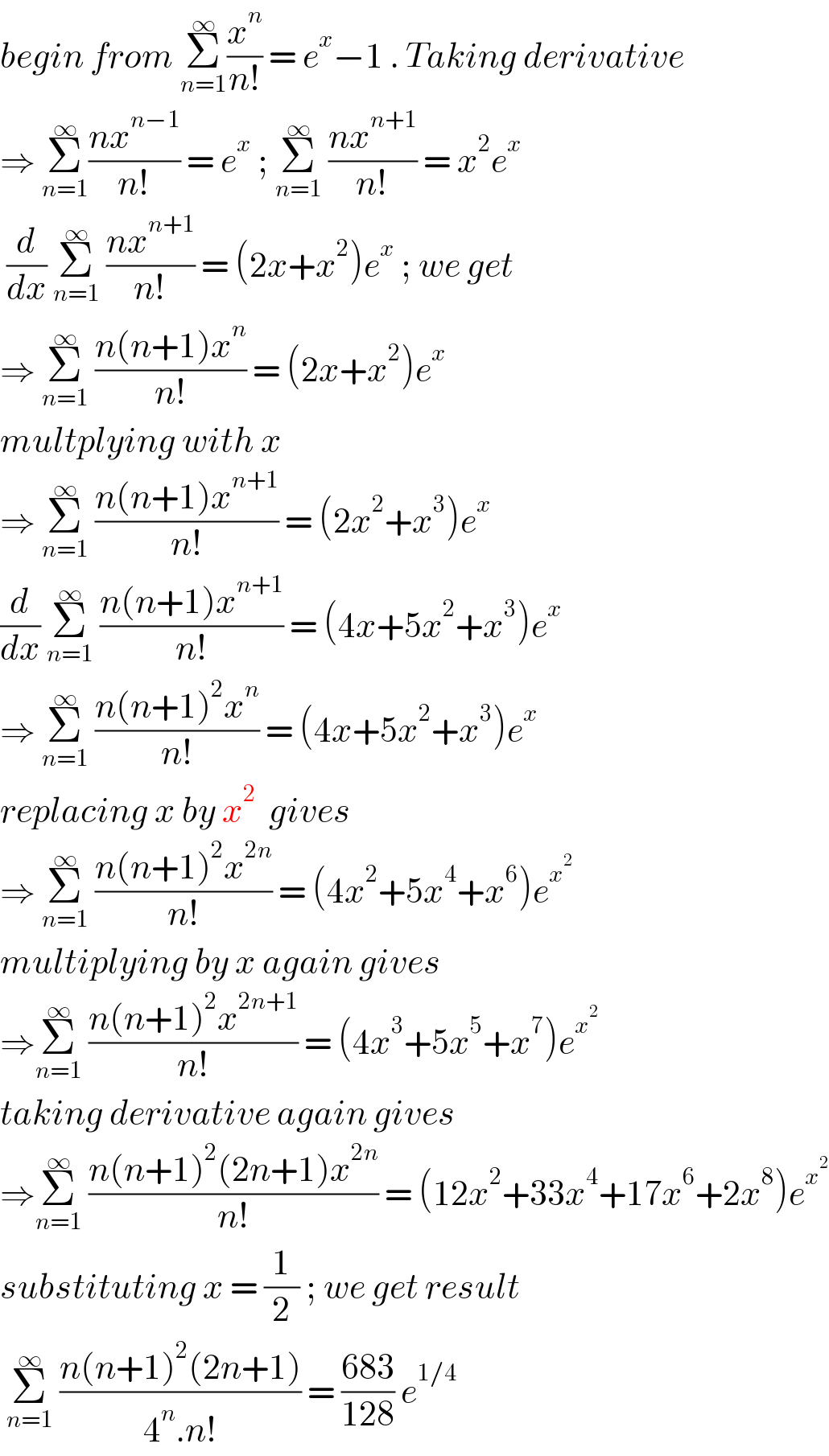
$${begin}\:{from}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}!}\:=\:{e}^{{x}} −\mathrm{1}\:.\:{Taking}\:{derivative} \\ $$$$\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{nx}^{{n}−\mathrm{1}} }{{n}!}\:=\:{e}^{{x}} \:;\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{nx}^{{n}+\mathrm{1}} }{{n}!}\:=\:{x}^{\mathrm{2}} {e}^{{x}} \\ $$$$\:\frac{{d}}{{dx}}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{nx}^{{n}+\mathrm{1}} }{{n}!}\:=\:\left(\mathrm{2}{x}+{x}^{\mathrm{2}} \right){e}^{{x}} \:;\:{we}\:{get} \\ $$$$\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{n}\left({n}+\mathrm{1}\right){x}^{{n}} }{{n}!}\:=\:\left(\mathrm{2}{x}+{x}^{\mathrm{2}} \right){e}^{{x}} \: \\ $$$${multplying}\:{with}\:{x}\: \\ $$$$\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{n}\left({n}+\mathrm{1}\right){x}^{{n}+\mathrm{1}} }{{n}!}\:=\:\left(\mathrm{2}{x}^{\mathrm{2}} +{x}^{\mathrm{3}} \right){e}^{{x}} \\ $$$$\frac{{d}}{{dx}}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{n}\left({n}+\mathrm{1}\right){x}^{{n}+\mathrm{1}} }{{n}!}\:=\:\left(\mathrm{4}{x}+\mathrm{5}{x}^{\mathrm{2}} +{x}^{\mathrm{3}} \right){e}^{{x}} \\ $$$$\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} {x}^{{n}} }{{n}!}\:=\:\left(\mathrm{4}{x}+\mathrm{5}{x}^{\mathrm{2}} +{x}^{\mathrm{3}} \right){e}^{{x}} \\ $$$${replacing}\:{x}\:{by}\:{x}^{\mathrm{2}} \:\:{gives}\: \\ $$$$\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} {x}^{\mathrm{2}{n}} }{{n}!}\:=\:\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{5}{x}^{\mathrm{4}} +{x}^{\mathrm{6}} \right){e}^{{x}^{\mathrm{2}} } \\ $$$${multiplying}\:{by}\:{x}\:{again}\:{gives} \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} {x}^{\mathrm{2}{n}+\mathrm{1}} }{{n}!}\:=\:\left(\mathrm{4}{x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{5}} +{x}^{\mathrm{7}} \right){e}^{{x}^{\mathrm{2}} } \\ $$$${taking}\:{derivative}\:{again}\:{gives} \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}{n}+\mathrm{1}\right){x}^{\mathrm{2}{n}} }{{n}!}\:=\:\left(\mathrm{12}{x}^{\mathrm{2}} +\mathrm{33}{x}^{\mathrm{4}} +\mathrm{17}{x}^{\mathrm{6}} +\mathrm{2}{x}^{\mathrm{8}} \right){e}^{{x}^{\mathrm{2}} } \\ $$$${substituting}\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:;\:{we}\:{get}\:{result}\: \\ $$$$\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{4}^{{n}} .{n}!}\:=\:\frac{\mathrm{683}}{\mathrm{128}}\:{e}^{\mathrm{1}/\mathrm{4}} \: \\ $$
Answered by Ñï= last updated on 09/Apr/21
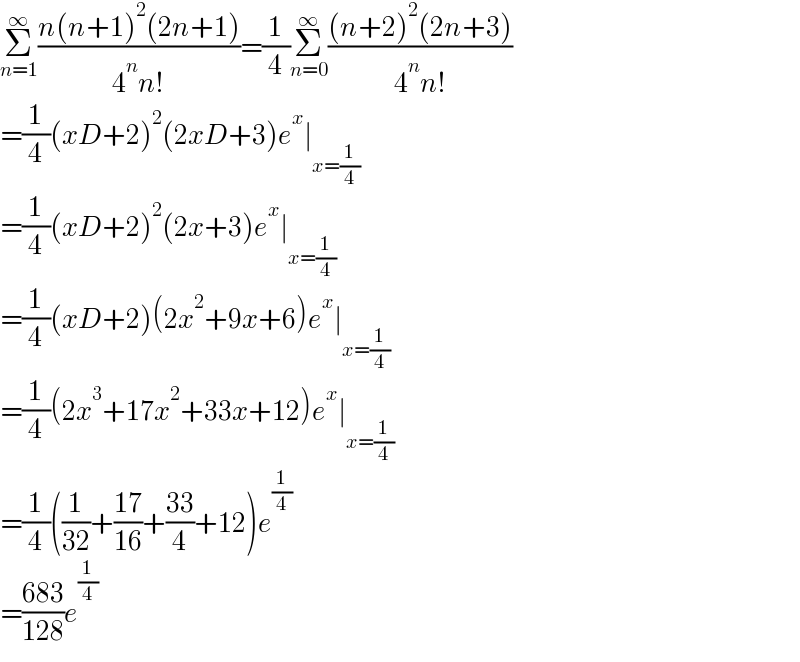
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{4}^{{n}} {n}!}=\frac{\mathrm{1}}{\mathrm{4}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({n}+\mathrm{2}\right)^{\mathrm{2}} \left(\mathrm{2}{n}+\mathrm{3}\right)}{\mathrm{4}^{{n}} {n}!} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left({xD}+\mathrm{2}\right)^{\mathrm{2}} \left(\mathrm{2}{xD}+\mathrm{3}\right){e}^{{x}} \mid_{{x}=\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left({xD}+\mathrm{2}\right)^{\mathrm{2}} \left(\mathrm{2}{x}+\mathrm{3}\right){e}^{{x}} \mid_{{x}=\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left({xD}+\mathrm{2}\right)\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{9}{x}+\mathrm{6}\right){e}^{{x}} \mid_{{x}=\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}{x}^{\mathrm{3}} +\mathrm{17}{x}^{\mathrm{2}} +\mathrm{33}{x}+\mathrm{12}\right){e}^{{x}} \mid_{{x}=\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{32}}+\frac{\mathrm{17}}{\mathrm{16}}+\frac{\mathrm{33}}{\mathrm{4}}+\mathrm{12}\right){e}^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{683}}{\mathrm{128}}{e}^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$
