Menu Close

Question-138024

Tinku Tara 0 Comments
Pin




Question Number 138024 by Algoritm last updated on 09/Apr/21
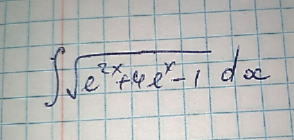
Answered by TheSupreme last updated on 09/Apr/21
e^x =u dx=(1/u)du ∫(√(u^2 +4u−1))(du/u) (u+2)=z ∫((√(z^2 −5))/(z−2))dz z^2 −5=w^2 dz=(w/( (√(w^2 +5))))dw ∫(w^2 /( (√(w^2 +5))))dw=w[(√(w^2 +5))]−∫(√(w^2 +5))dw w(√(w^2 +5))−(1/2)((√(w^2 +5))w+5sinh^(−1) ((w/( (√5)))))+c ((√(z^2 −5))/2)z+5sinh^(−1) (((√(z^2 −5))/( (√5))))+c ((√(u^2 +4u−1))/2)(u+2)+5sinh^(−1) (((√(u^2 +4u−1))/( (√5))))+c ((√(e^(2x) +4e^x −1))/2)(e^x +2)+5sinh^(−1) (((√(e^(2x) +4e^x −1))/( (√5))))+c
$${e}^{{x}} ={u} \\ $$$${dx}=\frac{\mathrm{1}}{{u}}{du} \\ $$$$\int\sqrt{{u}^{\mathrm{2}} +\mathrm{4}{u}−\mathrm{1}}\frac{{du}}{{u}} \\ $$$$\left({u}+\mathrm{2}\right)={z} \\ $$$$\int\frac{\sqrt{{z}^{\mathrm{2}} −\mathrm{5}}}{{z}−\mathrm{2}}{dz} \\ $$$${z}^{\mathrm{2}} −\mathrm{5}={w}^{\mathrm{2}} \\ $$$${dz}=\frac{{w}}{\:\sqrt{{w}^{\mathrm{2}} +\mathrm{5}}}{dw} \\ $$$$\int\frac{{w}^{\mathrm{2}} }{\:\sqrt{{w}^{\mathrm{2}} +\mathrm{5}}}{dw}={w}\left[\sqrt{{w}^{\mathrm{2}} +\mathrm{5}}\right]−\int\sqrt{{w}^{\mathrm{2}} +\mathrm{5}}{dw} \\ $$$${w}\sqrt{{w}^{\mathrm{2}} +\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{{w}^{\mathrm{2}} +\mathrm{5}}{w}+\mathrm{5}{sinh}^{−\mathrm{1}} \left(\frac{{w}}{\:\sqrt{\mathrm{5}}}\right)\right)+{c} \\ $$$$\frac{\sqrt{{z}^{\mathrm{2}} −\mathrm{5}}}{\mathrm{2}}{z}+\mathrm{5}{sinh}^{−\mathrm{1}} \left(\frac{\sqrt{{z}^{\mathrm{2}} −\mathrm{5}}}{\:\sqrt{\mathrm{5}}}\right)+{c} \\ $$$$\frac{\sqrt{{u}^{\mathrm{2}} +\mathrm{4}{u}−\mathrm{1}}}{\mathrm{2}}\left({u}+\mathrm{2}\right)+\mathrm{5}{sinh}^{−\mathrm{1}} \left(\frac{\sqrt{{u}^{\mathrm{2}} +\mathrm{4}{u}−\mathrm{1}}}{\:\sqrt{\mathrm{5}}}\right)+{c} \\ $$$$\frac{\sqrt{{e}^{\mathrm{2}{x}} +\mathrm{4}{e}^{{x}} −\mathrm{1}}}{\mathrm{2}}\left({e}^{{x}} +\mathrm{2}\right)+\mathrm{5}{sinh}^{−\mathrm{1}} \left(\frac{\sqrt{{e}^{\mathrm{2}{x}} +\mathrm{4}{e}^{{x}} −\mathrm{1}}}{\:\sqrt{\mathrm{5}}}\right)+{c} \\ $$
Answered by MJS_new last updated on 09/Apr/21
∫(√(e^(2x) +4e^x −1))dx=(√((e^x +2)^2 −5))dx= [t=((e^x +2+(√(e^(2x) +4e^x −1)))/( (√5))) → dx=((√(5(e^(2x) +4e^x −1)))/(e^x +2+(√(e^(2x) +4e^x −1))))] =(5/2)∫(((t^2 −1)^2 )/(t^2 ((√5)t^2 −4t+(√5))))dt= =∫(((√5)/(2t^2 ))+(2/t)+((√5)/2)−(2/( (√5)t^2 −4t+(√5))))dt= =−((√5)/(2t))+2ln t +(((√5)t)/2)−2arctan ((√5)t−2) = =(√(e^(2x) +4e^x −1))+2ln (e^x +2+(√(e^(2x) +4e^x −1))) −2arctan (e^x +(√(e^(2x) +4e^x −1))) +C
$$\int\sqrt{\mathrm{e}^{\mathrm{2}{x}} +\mathrm{4e}^{{x}} −\mathrm{1}}{dx}=\sqrt{\left(\mathrm{e}^{{x}} +\mathrm{2}\right)^{\mathrm{2}} −\mathrm{5}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\mathrm{e}^{{x}} +\mathrm{2}+\sqrt{\mathrm{e}^{\mathrm{2}{x}} +\mathrm{4e}^{{x}} −\mathrm{1}}}{\:\sqrt{\mathrm{5}}}\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{5}\left(\mathrm{e}^{\mathrm{2}{x}} +\mathrm{4e}^{{x}} −\mathrm{1}\right)}}{\mathrm{e}^{{x}} +\mathrm{2}+\sqrt{\mathrm{e}^{\mathrm{2}{x}} +\mathrm{4e}^{{x}} −\mathrm{1}}}\right] \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}\int\frac{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} \left(\sqrt{\mathrm{5}}{t}^{\mathrm{2}} −\mathrm{4}{t}+\sqrt{\mathrm{5}}\right)}{dt}= \\ $$$$=\int\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}{t}^{\mathrm{2}} }+\frac{\mathrm{2}}{{t}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}{t}^{\mathrm{2}} −\mathrm{4}{t}+\sqrt{\mathrm{5}}}\right){dt}= \\ $$$$=−\frac{\sqrt{\mathrm{5}}}{\mathrm{2}{t}}+\mathrm{2ln}\:{t}\:+\frac{\sqrt{\mathrm{5}}{t}}{\mathrm{2}}−\mathrm{2arctan}\:\left(\sqrt{\mathrm{5}}{t}−\mathrm{2}\right)\:= \\ $$$$=\sqrt{\mathrm{e}^{\mathrm{2}{x}} +\mathrm{4e}^{{x}} −\mathrm{1}}+\mathrm{2ln}\:\left(\mathrm{e}^{{x}} +\mathrm{2}+\sqrt{\mathrm{e}^{\mathrm{2}{x}} +\mathrm{4e}^{{x}} −\mathrm{1}}\right)\:−\mathrm{2arctan}\:\left(\mathrm{e}^{{x}} +\sqrt{\mathrm{e}^{\mathrm{2}{x}} +\mathrm{4e}^{{x}} −\mathrm{1}}\right)\:+{C} \\ $$
Answered by Mathspace last updated on 09/Apr/21
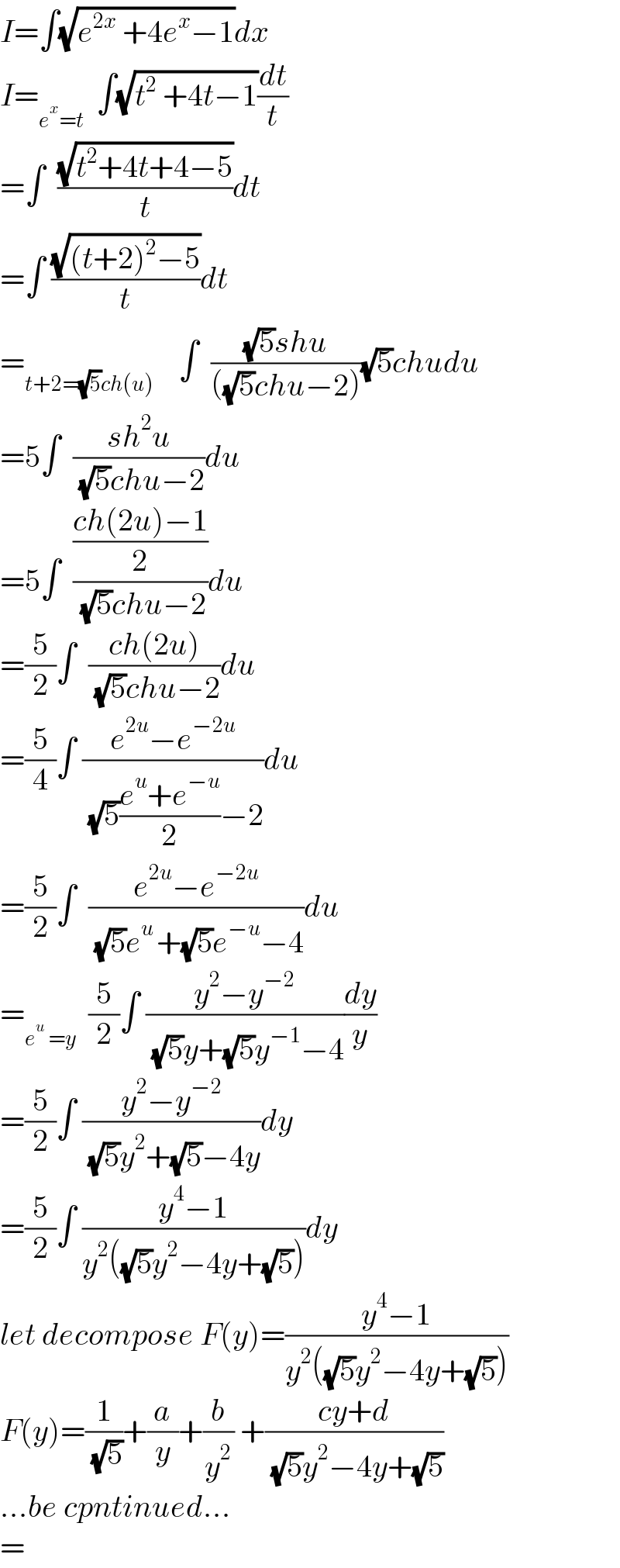
I=∫(√(e^(2x) +4e^x −1))dx I=_(e^x =t) ∫(√(t^2 +4t−1))(dt/t) =∫ ((√(t^2 +4t+4−5))/t)dt =∫ ((√((t+2)^2 −5))/t)dt =_(t+2=(√5)ch(u)) ∫ (((√5)shu)/(((√5)chu−2)))(√5)chudu =5∫ ((sh^2 u)/( (√5)chu−2))du =5∫ (((ch(2u)−1)/2)/( (√5)chu−2))du =(5/2)∫ ((ch(2u))/( (√5)chu−2))du =(5/4)∫ ((e^(2u) −e^(−2u) )/( (√5)((e^u +e^(−u) )/2)−2))du =(5/2)∫ ((e^(2u) −e^(−2u) )/( (√5)e^(u ) +(√5)e^(−u) −4))du =_(e^u =y) (5/2)∫ ((y^2 −y^(−2) )/( (√5)y+(√5)y^(−1) −4))(dy/y) =(5/2)∫ ((y^2 −y^(−2) )/( (√5)y^2 +(√5)−4y))dy =(5/2)∫ ((y^4 −1)/(y^2 ((√5)y^2 −4y+(√5))))dy let decompose F(y)=((y^4 −1)/(y^2 ((√5)y^2 −4y+(√5)))) F(y)=(1/( (√5)))+(a/y)+(b/y^2 ) +((cy+d)/( (√5)y^2 −4y+(√5))) ...be cpntinued... =
$${I}=\int\sqrt{{e}^{\mathrm{2}{x}} \:+\mathrm{4}{e}^{{x}} −\mathrm{1}}{dx} \\ $$$${I}=_{{e}^{{x}} ={t}} \:\:\int\sqrt{{t}^{\mathrm{2}} \:+\mathrm{4}{t}−\mathrm{1}}\frac{{dt}}{{t}} \\ $$$$=\int\:\:\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{4}{t}+\mathrm{4}−\mathrm{5}}}{{t}}{dt} \\ $$$$=\int\:\frac{\sqrt{\left({t}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{5}}}{{t}}{dt} \\ $$$$=_{{t}+\mathrm{2}=\sqrt{\mathrm{5}}{ch}\left({u}\right)} \:\:\:\:\int\:\:\frac{\sqrt{\mathrm{5}}{shu}}{\left(\sqrt{\mathrm{5}}{chu}−\mathrm{2}\right)}\sqrt{\mathrm{5}}{chudu} \\ $$$$=\mathrm{5}\int\:\:\frac{{sh}^{\mathrm{2}} {u}}{\:\sqrt{\mathrm{5}}{chu}−\mathrm{2}}{du} \\ $$$$=\mathrm{5}\int\:\:\frac{\frac{{ch}\left(\mathrm{2}{u}\right)−\mathrm{1}}{\mathrm{2}}}{\:\sqrt{\mathrm{5}}{chu}−\mathrm{2}}{du} \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}\int\:\:\frac{{ch}\left(\mathrm{2}{u}\right)}{\:\sqrt{\mathrm{5}}{chu}−\mathrm{2}}{du} \\ $$$$=\frac{\mathrm{5}}{\mathrm{4}}\int\:\frac{{e}^{\mathrm{2}{u}} −{e}^{−\mathrm{2}{u}} }{\:\sqrt{\mathrm{5}}\frac{{e}^{{u}} +{e}^{−{u}} }{\mathrm{2}}−\mathrm{2}}{du} \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}\int\:\:\frac{{e}^{\mathrm{2}{u}} −{e}^{−\mathrm{2}{u}} }{\:\sqrt{\mathrm{5}}{e}^{{u}\:} +\sqrt{\mathrm{5}}{e}^{−{u}} −\mathrm{4}}{du} \\ $$$$=_{{e}^{{u}} \:={y}} \:\:\frac{\mathrm{5}}{\mathrm{2}}\int\:\frac{{y}^{\mathrm{2}} −{y}^{−\mathrm{2}} }{\:\sqrt{\mathrm{5}}{y}+\sqrt{\mathrm{5}}{y}^{−\mathrm{1}} −\mathrm{4}}\frac{{dy}}{{y}} \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}\int\:\frac{{y}^{\mathrm{2}} −{y}^{−\mathrm{2}} }{\:\sqrt{\mathrm{5}}{y}^{\mathrm{2}} +\sqrt{\mathrm{5}}−\mathrm{4}{y}}{dy} \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}\int\:\frac{{y}^{\mathrm{4}} −\mathrm{1}}{{y}^{\mathrm{2}} \left(\sqrt{\mathrm{5}}{y}^{\mathrm{2}} −\mathrm{4}{y}+\sqrt{\mathrm{5}}\right)}{dy} \\ $$$${let}\:{decompose}\:{F}\left({y}\right)=\frac{{y}^{\mathrm{4}} −\mathrm{1}}{{y}^{\mathrm{2}} \left(\sqrt{\mathrm{5}}{y}^{\mathrm{2}} −\mathrm{4}{y}+\sqrt{\mathrm{5}}\right)} \\ $$$${F}\left({y}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}+\frac{{a}}{{y}}+\frac{{b}}{{y}^{\mathrm{2}} }\:+\frac{{cy}+{d}}{\:\sqrt{\mathrm{5}}{y}^{\mathrm{2}} −\mathrm{4}{y}+\sqrt{\mathrm{5}}} \\ $$$$…{be}\:{cpntinued}… \\ $$$$= \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *