Question Number 138062 by I want to learn more last updated on 09/Apr/21

Answered by mr W last updated on 09/Apr/21
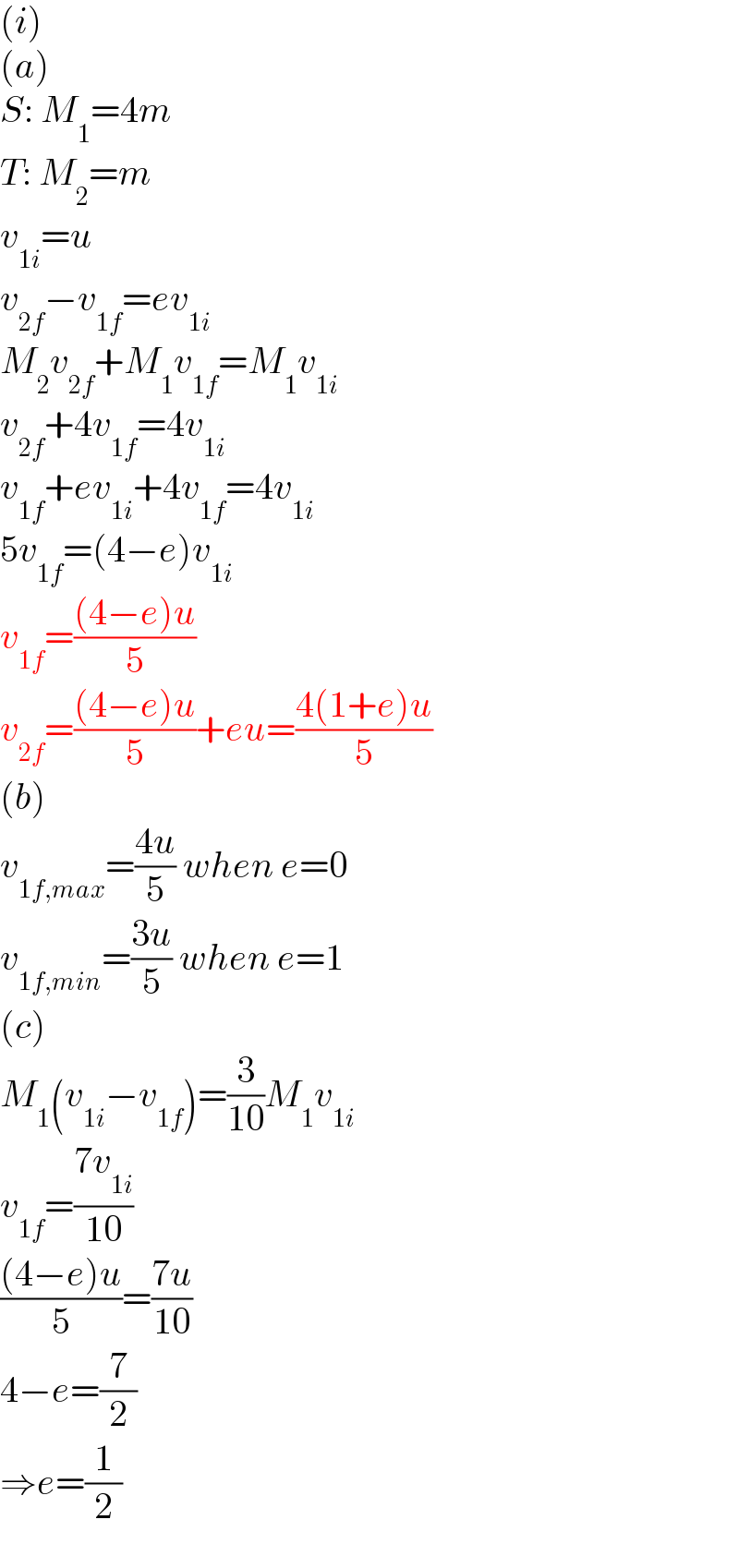
$$\left({i}\right) \\ $$$$\left({a}\right) \\ $$$${S}:\:{M}_{\mathrm{1}} =\mathrm{4}{m} \\ $$$${T}:\:{M}_{\mathrm{2}} ={m} \\ $$$${v}_{\mathrm{1}{i}} ={u} \\ $$$${v}_{\mathrm{2}{f}} −{v}_{\mathrm{1}{f}} ={ev}_{\mathrm{1}{i}} \\ $$$${M}_{\mathrm{2}} {v}_{\mathrm{2}{f}} +{M}_{\mathrm{1}} {v}_{\mathrm{1}{f}} ={M}_{\mathrm{1}} {v}_{\mathrm{1}{i}} \\ $$$${v}_{\mathrm{2}{f}} +\mathrm{4}{v}_{\mathrm{1}{f}} =\mathrm{4}{v}_{\mathrm{1}{i}} \\ $$$${v}_{\mathrm{1}{f}} +{ev}_{\mathrm{1}{i}} +\mathrm{4}{v}_{\mathrm{1}{f}} =\mathrm{4}{v}_{\mathrm{1}{i}} \\ $$$$\mathrm{5}{v}_{\mathrm{1}{f}} =\left(\mathrm{4}−{e}\right){v}_{\mathrm{1}{i}} \\ $$$${v}_{\mathrm{1}{f}} =\frac{\left(\mathrm{4}−{e}\right){u}}{\mathrm{5}} \\ $$$${v}_{\mathrm{2}{f}} =\frac{\left(\mathrm{4}−{e}\right){u}}{\mathrm{5}}+{eu}=\frac{\mathrm{4}\left(\mathrm{1}+{e}\right){u}}{\mathrm{5}} \\ $$$$\left({b}\right) \\ $$$${v}_{\mathrm{1}{f},{max}} =\frac{\mathrm{4}{u}}{\mathrm{5}}\:{when}\:{e}=\mathrm{0} \\ $$$${v}_{\mathrm{1}{f},{min}} =\frac{\mathrm{3}{u}}{\mathrm{5}}\:{when}\:{e}=\mathrm{1} \\ $$$$\left({c}\right) \\ $$$${M}_{\mathrm{1}} \left({v}_{\mathrm{1}{i}} −{v}_{\mathrm{1}{f}} \right)=\frac{\mathrm{3}}{\mathrm{10}}{M}_{\mathrm{1}} {v}_{\mathrm{1}{i}} \\ $$$${v}_{\mathrm{1}{f}} =\frac{\mathrm{7}{v}_{\mathrm{1}{i}} }{\mathrm{10}} \\ $$$$\frac{\left(\mathrm{4}−{e}\right){u}}{\mathrm{5}}=\frac{\mathrm{7}{u}}{\mathrm{10}} \\ $$$$\mathrm{4}−{e}=\frac{\mathrm{7}}{\mathrm{2}} \\ $$$$\Rightarrow{e}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by I want to learn more last updated on 10/Apr/21
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Answered by mr W last updated on 10/Apr/21
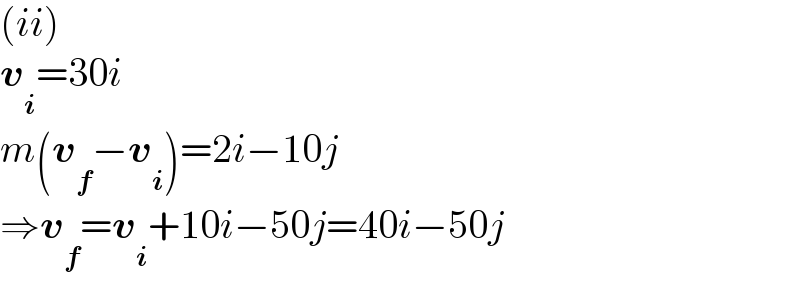
$$\left({ii}\right) \\ $$$$\boldsymbol{{v}}_{\boldsymbol{{i}}} =\mathrm{30}{i} \\ $$$${m}\left(\boldsymbol{{v}}_{\boldsymbol{{f}}} −\boldsymbol{{v}}_{\boldsymbol{{i}}} \right)=\mathrm{2}{i}−\mathrm{10}{j} \\ $$$$\Rightarrow\boldsymbol{{v}}_{\boldsymbol{{f}}} =\boldsymbol{{v}}_{\boldsymbol{{i}}} +\mathrm{10}{i}−\mathrm{50}{j}=\mathrm{40}{i}−\mathrm{50}{j} \\ $$
Commented by I want to learn more last updated on 10/Apr/21
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
