Question Number 138154 by JulioCesar last updated on 10/Apr/21

Answered by TheSupreme last updated on 10/Apr/21
![((x^2 +1−2x)/x)≥(1−x)^3 (((x−1)^2 )/x)≥(1−x)^3 (x−1)^2 [(1/x)−(1−x)]≥0 (x−1)^2 [((1−x+x^2 )/x)]≥0 (x−1)≥0 ∀x x>0 x^2 −x+1≥0 ∀x so thd reation is true for x>0](https://www.tinkutara.com/question/Q138156.png)
$$\frac{{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{x}}{{x}}\geqslant\left(\mathrm{1}−{x}\right)^{\mathrm{3}} \\ $$$$\frac{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }{{x}}\geqslant\left(\mathrm{1}−{x}\right)^{\mathrm{3}} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left[\frac{\mathrm{1}}{{x}}−\left(\mathrm{1}−{x}\right)\right]\geqslant\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left[\frac{\mathrm{1}−{x}+{x}^{\mathrm{2}} }{{x}}\right]\geqslant\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\geqslant\mathrm{0}\:\forall{x} \\ $$$${x}>\mathrm{0} \\ $$$${x}^{\mathrm{2}} −{x}+\mathrm{1}\geqslant\mathrm{0}\:\forall{x} \\ $$$$ \\ $$$${so}\:{thd}\:{reation}\:{is}\:{true}\:{for}\:{x}>\mathrm{0} \\ $$
Commented by MJS_new last updated on 10/Apr/21
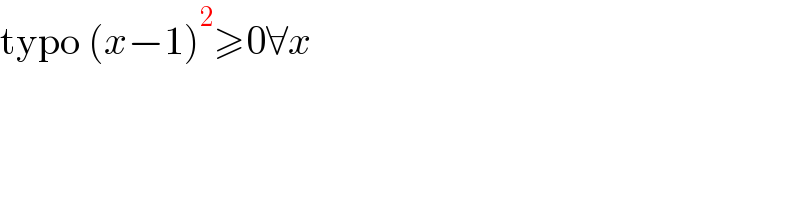
$$\mathrm{typo}\:\left({x}−\mathrm{1}\right)^{\mathrm{2}} \geqslant\mathrm{0}\forall{x} \\ $$
