Question Number 138159 by BHOOPENDRA last updated on 10/Apr/21

Answered by Dwaipayan Shikari last updated on 10/Apr/21
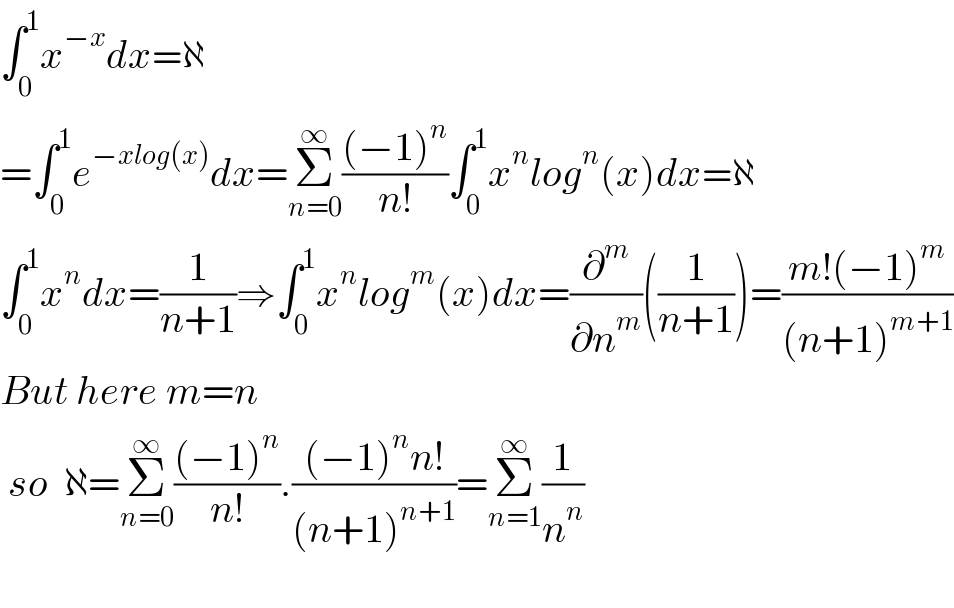
$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{−{x}} {dx}=\aleph \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−{xlog}\left({x}\right)} {dx}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} {log}^{{n}} \left({x}\right){dx}=\aleph \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} {dx}=\frac{\mathrm{1}}{{n}+\mathrm{1}}\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} {log}^{{m}} \left({x}\right){dx}=\frac{\partial^{{m}} }{\partial{n}^{{m}} }\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)=\frac{{m}!\left(−\mathrm{1}\right)^{{m}} }{\left({n}+\mathrm{1}\right)^{{m}+\mathrm{1}} } \\ $$$${But}\:{here}\:{m}={n} \\ $$$$\:{so}\:\:\aleph=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}.\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{{n}} } \\ $$$$ \\ $$
