Question Number 138205 by Bekzod Jumayev last updated on 11/Apr/21

Commented by Jamshidbek last updated on 11/Apr/21

$$\mathrm{Og}'\mathrm{ayni}\:\mathrm{kun}\:\mathrm{savolini}\:\mathrm{oziz}\:\mathrm{yechmasizmi}? \\ $$$$\mathrm{Yoki}\:\mathrm{kechqurun}\:\mathrm{kanalga}\:\mathrm{tashlanadiku}\:\mathrm{yechim}.\mathrm{O}'\mathrm{shanda} \\ $$$$\mathrm{o}'\mathrm{rganib}\:\mathrm{olardizda} \\ $$
Commented by Bekzod Jumayev last updated on 13/Apr/21

$${Uzur}\:{yechimni}\:{o}'{rganmoqchi}\:{edim} \\ $$$${kanalga}\:{joylash}\:{niyatim}\:{yoq}\:{edi} \\ $$$$ \\ $$
Commented by Jamshidbek last updated on 13/Apr/21

$$\mathrm{Uzr}\:\mathrm{men}\:\mathrm{noto}'\mathrm{g}'\mathrm{ri}\:\mathrm{tushunib}\:\mathrm{olibman}.\mathrm{Men} \\ $$$$\mathrm{sizni}\:\mathrm{kanalga}\:\mathrm{joylash}\:\mathrm{uchun}\:\mathrm{so}'\mathrm{rayapti} \\ $$$$\mathrm{deb}\:\mathrm{o}'\mathrm{ylabman}.\mathrm{Uzr}\:\mathrm{ming}\:\mathrm{bor} \\ $$
Answered by phanphuoc last updated on 11/Apr/21
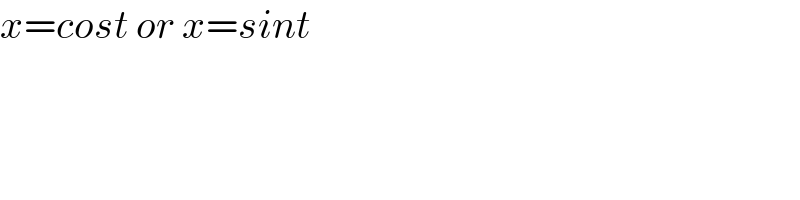
$${x}={cost}\:{or}\:{x}={sint} \\ $$$$ \\ $$
Answered by MJS_new last updated on 11/Apr/21
![∫(x^2 /(x+(√(1−x^2 ))))dx= [t=(x/( (√(1−x^2 )))) → dx=(1−x^2 )^(3/2) dt] =∫(t^2 /((t+1)(t^2 +1)^2 ))dt= [Ostrogradski′s Method] =−((t+1)/(4(t^2 +1)))−(1/4)∫((t−1)/((t+1)(t^2 +1)))dt= =−((t+1)/(4(t^2 +1)))+(1/4)∫(1/(t+1))−(t/(t^2 +1))dt= =−((t+1)/(4(t^2 +1)))+(1/4)ln (t+1) −(1/8)ln (t^2 +1) = =−((t+1)/(4(t^2 +1)))+(1/8)ln (((t+1)^2 )/(t^2 +1)) = =((x^2 −1−x(√(1−x^2 )))/4)+(1/4)ln (x+(√(1−x^2 ))) +C ⇒ answer is (1/4)](https://www.tinkutara.com/question/Q138226.png)
$$\int\frac{{x}^{\mathrm{2}} }{{x}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\rightarrow\:{dx}=\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} {dt}\right] \\ $$$$=\int\frac{{t}^{\mathrm{2}} }{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=−\frac{{t}+\mathrm{1}}{\mathrm{4}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{t}−\mathrm{1}}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{dt}= \\ $$$$=−\frac{{t}+\mathrm{1}}{\mathrm{4}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{1}}{{t}+\mathrm{1}}−\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}= \\ $$$$=−\frac{{t}+\mathrm{1}}{\mathrm{4}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left({t}+\mathrm{1}\right)\:−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +\mathrm{1}\right)\:= \\ $$$$=−\frac{{t}+\mathrm{1}}{\mathrm{4}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{ln}\:\frac{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} +\mathrm{1}}\:= \\ $$$$=\frac{{x}^{\mathrm{2}} −\mathrm{1}−{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left({x}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)\:+{C} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$
