Question Number 138206 by Bekzod Jumayev last updated on 11/Apr/21

Commented by Bekzod Jumayev last updated on 11/Apr/21

$${Help}? \\ $$
Answered by mr W last updated on 11/Apr/21
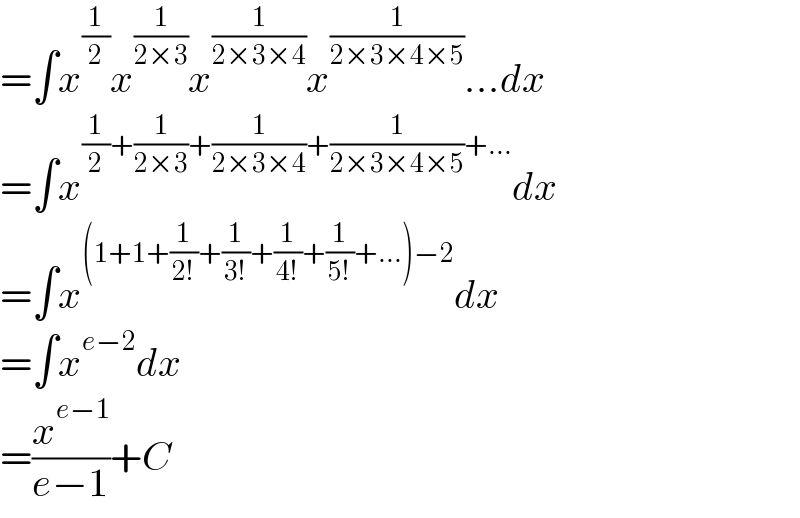
$$=\int{x}^{\frac{\mathrm{1}}{\mathrm{2}}} {x}^{\frac{\mathrm{1}}{\mathrm{2}×\mathrm{3}}} {x}^{\frac{\mathrm{1}}{\mathrm{2}×\mathrm{3}×\mathrm{4}}} {x}^{\frac{\mathrm{1}}{\mathrm{2}×\mathrm{3}×\mathrm{4}×\mathrm{5}}} …{dx} \\ $$$$=\int{x}^{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}×\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}×\mathrm{3}×\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}×\mathrm{3}×\mathrm{4}×\mathrm{5}}+…} {dx} \\ $$$$=\int{x}^{\left(\mathrm{1}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}+\frac{\mathrm{1}}{\mathrm{5}!}+…\right)−\mathrm{2}} {dx} \\ $$$$=\int{x}^{{e}−\mathrm{2}} {dx} \\ $$$$=\frac{{x}^{{e}−\mathrm{1}} }{{e}−\mathrm{1}}+{C} \\ $$
