Question Number 138224 by Bekzod Jumayev last updated on 11/Apr/21
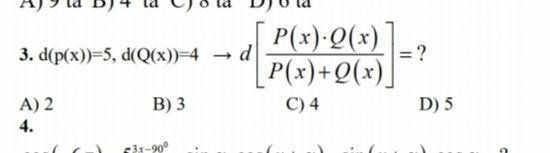
Commented by Bekzod Jumayev last updated on 11/Apr/21

$${Help} \\ $$
Answered by MJS_new last updated on 11/Apr/21
![(d/dx)[p(x)]=5 ⇒ p(x)=5x+C_1 (d/dx)[q(x)]=4 ⇒ q(x)=4x+C_2 we can only solve if we know C_1 , C_2 if C_1 =C_2 =0 (d/dx)[((p(x)q(x))/(p(x)+q(x)))]=(d/dx)[((20x^2 )/(9x))]=(d/dx)[((20x)/9)]=((20)/9)](https://www.tinkutara.com/question/Q138228.png)
$$\frac{{d}}{{dx}}\left[{p}\left({x}\right)\right]=\mathrm{5}\:\Rightarrow\:{p}\left({x}\right)=\mathrm{5}{x}+{C}_{\mathrm{1}} \\ $$$$\frac{{d}}{{dx}}\left[{q}\left({x}\right)\right]=\mathrm{4}\:\Rightarrow\:{q}\left({x}\right)=\mathrm{4}{x}+{C}_{\mathrm{2}} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{only}\:\mathrm{solve}\:\mathrm{if}\:\mathrm{we}\:\mathrm{know}\:{C}_{\mathrm{1}} ,\:{C}_{\mathrm{2}} \\ $$$$\mathrm{if}\:{C}_{\mathrm{1}} ={C}_{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{{d}}{{dx}}\left[\frac{{p}\left({x}\right){q}\left({x}\right)}{{p}\left({x}\right)+{q}\left({x}\right)}\right]=\frac{{d}}{{dx}}\left[\frac{\mathrm{20}{x}^{\mathrm{2}} }{\mathrm{9}{x}}\right]=\frac{{d}}{{dx}}\left[\frac{\mathrm{20}{x}}{\mathrm{9}}\right]=\frac{\mathrm{20}}{\mathrm{9}} \\ $$
