Question Number 138254 by mey3nipaba last updated on 11/Apr/21

Commented by Rasheed.Sindhi last updated on 11/Apr/21

$$\mathrm{40} \\ $$
Commented by Dwaipayan Shikari last updated on 11/Apr/21

$$\mathrm{4}×\mathrm{1}+\mathrm{1}=\mathrm{5} \\ $$$$\mathrm{2}×\mathrm{5}+\mathrm{2}=\mathrm{12} \\ $$$$\mathrm{3}×\mathrm{6}+\mathrm{3}=\mathrm{21} \\ $$$$\mathrm{8}×\mathrm{11}+\mathrm{8}=\mathrm{96} \\ $$
Commented by mey3nipaba last updated on 11/Apr/21

$${please}\:{i}\:{understand}\:{the}\:{process}\:{you}\:{used}\:{but}\: \\ $$$${don}'{t}\:{you}\:{think}\:{there}'{s}\:{the}\:{need}\:{to}\:{continue} \\ $$$${from}\:\mathrm{4}+\mathrm{7},\mathrm{5}+\mathrm{8},\mathrm{6}+\mathrm{9},…\:{till}\:{you}\:{get}\:{to}\:\mathrm{8}+\mathrm{11}=? \\ $$
Commented by mey3nipaba last updated on 11/Apr/21

$${oh}\:{okay}\:{thanks} \\ $$
Commented by Rasheed.Sindhi last updated on 11/Apr/21
$${Nice}! \\ $$$${I}\:{think}\:{you}'{ve}\:{found}\:{better}\:{relation} \\ $$$${than}\:{I}'{ve}! \\ $$
Commented by Dwaipayan Shikari last updated on 11/Apr/21
$${What}\:{was}\:{your}\:{relation}\:{sir}? \\ $$
Commented by EDWIN88 last updated on 12/Apr/21
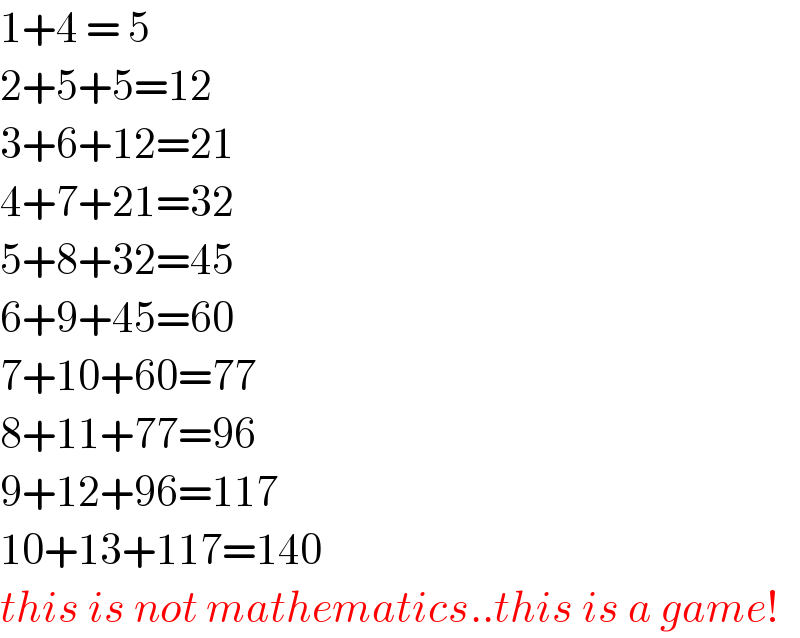
$$\mathrm{1}+\mathrm{4}\:=\:\mathrm{5} \\ $$$$\mathrm{2}+\mathrm{5}+\mathrm{5}=\mathrm{12} \\ $$$$\mathrm{3}+\mathrm{6}+\mathrm{12}=\mathrm{21} \\ $$$$\mathrm{4}+\mathrm{7}+\mathrm{21}=\mathrm{32} \\ $$$$\mathrm{5}+\mathrm{8}+\mathrm{32}=\mathrm{45} \\ $$$$\mathrm{6}+\mathrm{9}+\mathrm{45}=\mathrm{60} \\ $$$$\mathrm{7}+\mathrm{10}+\mathrm{60}=\mathrm{77} \\ $$$$\mathrm{8}+\mathrm{11}+\mathrm{77}=\mathrm{96} \\ $$$$\mathrm{9}+\mathrm{12}+\mathrm{96}=\mathrm{117} \\ $$$$\mathrm{10}+\mathrm{13}+\mathrm{117}=\mathrm{140} \\ $$$${this}\:{is}\:{not}\:{mathematics}..{this}\:{is}\:{a}\:{game}! \\ $$
Commented by greg_ed last updated on 12/Apr/21
$$\left.\mathrm{mathematic}\:\mathrm{is}\:\mathrm{a}\:\mathrm{game}\:!\::\right) \\ $$
Commented by Rasheed.Sindhi last updated on 12/Apr/21
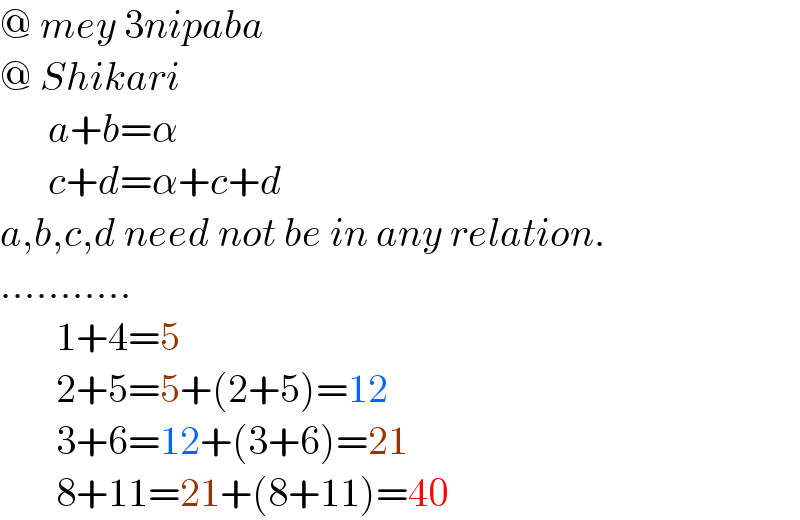
$$@\:{mey}\:\mathrm{3}{nipaba} \\ $$$$@\:{Shikari} \\ $$$$\:\:\:\:\:\:{a}+{b}=\alpha \\ $$$$\:\:\:\:\:\:{c}+{d}=\alpha+{c}+{d} \\ $$$${a},{b},{c},{d}\:{need}\:{not}\:{be}\:{in}\:{any}\:{relation}. \\ $$$$……….. \\ $$$$\:\:\:\:\:\:\:\mathrm{1}+\mathrm{4}=\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\mathrm{2}+\mathrm{5}=\mathrm{5}+\left(\mathrm{2}+\mathrm{5}\right)=\mathrm{12} \\ $$$$\:\:\:\:\:\:\:\mathrm{3}+\mathrm{6}=\mathrm{12}+\left(\mathrm{3}+\mathrm{6}\right)=\mathrm{21} \\ $$$$\:\:\:\:\:\:\:\mathrm{8}+\mathrm{11}=\mathrm{21}+\left(\mathrm{8}+\mathrm{11}\right)=\mathrm{40} \\ $$
Commented by MJS_new last updated on 12/Apr/21

$$\mathrm{obviously}\:“+''\:\mathrm{is}\:\mathrm{not}\:\mathrm{the}\:\mathrm{usual}\:\mathrm{operation}\:+ \\ $$$$\Rightarrow \\ $$$$\mathrm{we}\:\mathrm{must}\:\mathrm{find}\:\mathrm{an}\:\mathrm{operation}\:\blacksquare\:\mathrm{with} \\ $$$$\mathrm{1}\blacksquare\mathrm{4}=\mathrm{5}\wedge\mathrm{2}\blacksquare\mathrm{5}=\mathrm{12}\wedge\mathrm{3}\blacksquare\mathrm{6}=\mathrm{21} \\ $$$$\mathrm{if}\:\blacksquare\:\mathrm{is}\:\mathrm{unique}\:\mathrm{we}\:\mathrm{can}\:\mathrm{give}\:\mathrm{the}\:\mathrm{result}\:\mathrm{for} \\ $$$$\mathrm{8}\blacksquare\mathrm{11}={x},\:\mathrm{otherwise}\:{x}\:\mathrm{can}\:\mathrm{be}\:\mathrm{any}\:\mathrm{number} \\ $$
