Question Number 138278 by 676597498 last updated on 11/Apr/21

Answered by TheSupreme last updated on 12/Apr/21
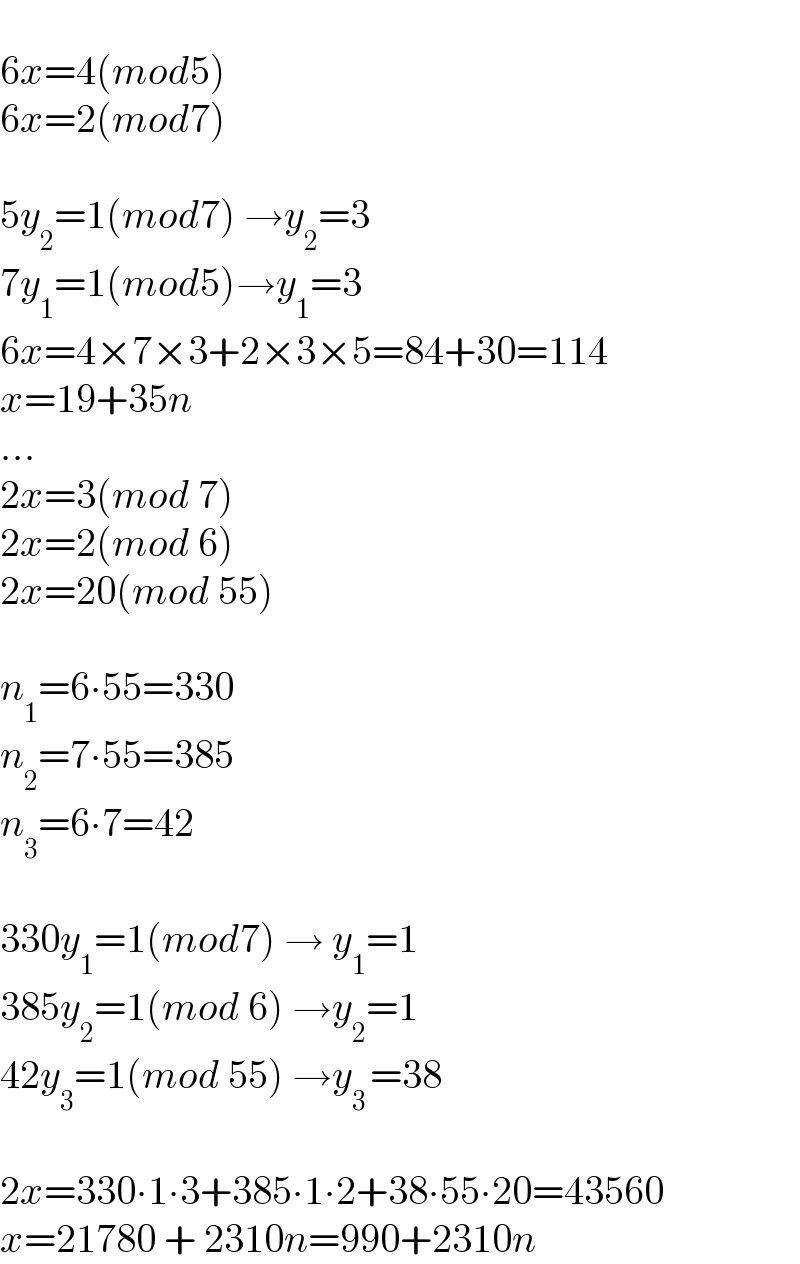
$$ \\ $$$$\mathrm{6}{x}=\mathrm{4}\left({mod}\mathrm{5}\right) \\ $$$$\mathrm{6}{x}=\mathrm{2}\left({mod}\mathrm{7}\right) \\ $$$$ \\ $$$$\mathrm{5}{y}_{\mathrm{2}} =\mathrm{1}\left({mod}\mathrm{7}\right)\:\rightarrow{y}_{\mathrm{2}} =\mathrm{3} \\ $$$$\mathrm{7}{y}_{\mathrm{1}} =\mathrm{1}\left({mod}\mathrm{5}\right)\rightarrow{y}_{\mathrm{1}} =\mathrm{3} \\ $$$$\mathrm{6}{x}=\mathrm{4}×\mathrm{7}×\mathrm{3}+\mathrm{2}×\mathrm{3}×\mathrm{5}=\mathrm{84}+\mathrm{30}=\mathrm{114} \\ $$$${x}=\mathrm{19}+\mathrm{35}{n} \\ $$$$… \\ $$$$\mathrm{2}{x}=\mathrm{3}\left({mod}\:\mathrm{7}\right) \\ $$$$\mathrm{2}{x}=\mathrm{2}\left({mod}\:\mathrm{6}\right) \\ $$$$\mathrm{2}{x}=\mathrm{20}\left({mod}\:\mathrm{55}\right) \\ $$$$ \\ $$$${n}_{\mathrm{1}} =\mathrm{6}\centerdot\mathrm{55}=\mathrm{330} \\ $$$${n}_{\mathrm{2}} =\mathrm{7}\centerdot\mathrm{55}=\mathrm{385} \\ $$$${n}_{\mathrm{3}} =\mathrm{6}\centerdot\mathrm{7}=\mathrm{42} \\ $$$$ \\ $$$$\mathrm{330}{y}_{\mathrm{1}} =\mathrm{1}\left({mod}\mathrm{7}\right)\:\rightarrow\:{y}_{\mathrm{1}} =\mathrm{1} \\ $$$$\mathrm{385}{y}_{\mathrm{2}} =\mathrm{1}\left({mod}\:\mathrm{6}\right)\:\rightarrow{y}_{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{42}{y}_{\mathrm{3}} =\mathrm{1}\left({mod}\:\mathrm{55}\right)\:\rightarrow{y}_{\mathrm{3}\:} =\mathrm{38}\: \\ $$$$ \\ $$$$\mathrm{2}{x}=\mathrm{330}\centerdot\mathrm{1}\centerdot\mathrm{3}+\mathrm{385}\centerdot\mathrm{1}\centerdot\mathrm{2}+\mathrm{38}\centerdot\mathrm{55}\centerdot\mathrm{20}=\mathrm{43560} \\ $$$${x}=\mathrm{21780}\:+\:\mathrm{2310}{n}=\mathrm{990}+\mathrm{2310}{n} \\ $$
