Question Number 138320 by aliibrahim1 last updated on 12/Apr/21
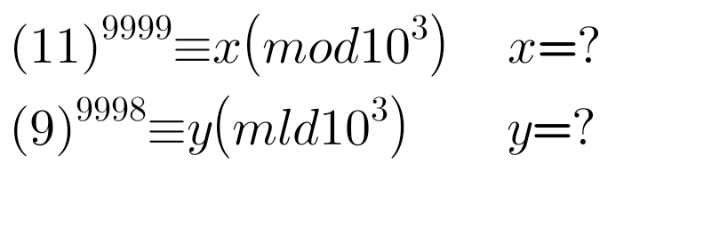
Answered by Rasheed.Sindhi last updated on 17/Apr/21

$$\mathrm{11}^{{n}} =\left(\mathrm{1}+\mathrm{10}\right)^{{n}} =\begin{pmatrix}{{n}}\\{\mathrm{0}}\end{pmatrix}\left(\mathrm{10}\right)^{\mathrm{0}} +\begin{pmatrix}{{n}}\\{\mathrm{1}}\end{pmatrix}\left(\mathrm{10}\right)^{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:+\begin{pmatrix}{{n}}\\{\mathrm{2}}\end{pmatrix}\left(\mathrm{10}\right)^{\mathrm{2}} +\underset{{divisible}\:{by}\:\mathrm{1000}} {\underbrace{\begin{pmatrix}{{n}}\\{\mathrm{3}}\end{pmatrix}\left(\mathrm{10}\right)^{\mathrm{3}} ….+\begin{pmatrix}{{n}}\\{{n}}\end{pmatrix}\left(\mathrm{10}\right)^{{n}} }} \\ $$$$\smile\frown\smile\frown\smile\frown\smile\frown\smile\frown\smile\frown\smile\frown \\ $$$$\left(\mathrm{11}\right)^{\mathrm{9999}} \equiv{x}\left({mod}\:\mathrm{1000}\right) \\ $$$$\left(\mathrm{1}+\mathrm{10}\right)^{\mathrm{9999}} \equiv\begin{pmatrix}{\mathrm{9999}}\\{\:\:\:\:\mathrm{0}}\end{pmatrix}\left(\mathrm{10}\right)^{\mathrm{0}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\begin{pmatrix}{\mathrm{9999}}\\{\:\:\:\:\mathrm{1}}\end{pmatrix}\left(\mathrm{10}\right)^{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\begin{pmatrix}{\mathrm{9999}}\\{\:\:\:\:\mathrm{2}}\end{pmatrix}\left(\mathrm{10}\right)^{\mathrm{2}} \left({md}\mathrm{1000}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\equiv\mathrm{1}+\mathrm{99990}+\mathrm{4998500100} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\equiv\mathrm{4998600091}\equiv\mathrm{91} \\ $$
Commented by aliibrahim1 last updated on 27/Apr/21

$${thx}\:{man} \\ $$
