Menu Close

Question-138336

Tinku Tara 0 Comments
Pin




Question Number 138336 by mr W last updated on 12/Apr/21
Commented by mr W last updated on 12/Apr/21
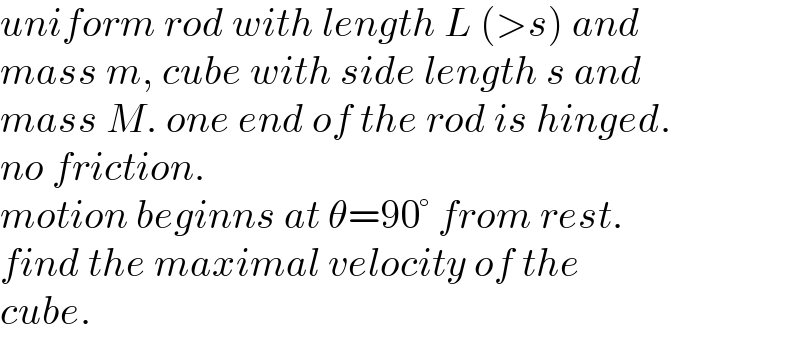
uniform rod with length L (>s) and mass m, cube with side length s and mass M. one end of the rod is hinged. no friction. motion beginns at θ=90° from rest. find the maximal velocity of the cube.
$${uniform}\:{rod}\:{with}\:{length}\:{L}\:\left(>{s}\right)\:{and}\: \\ $$$${mass}\:{m},\:{cube}\:{with}\:{side}\:{length}\:{s}\:{and}\: \\ $$$${mass}\:{M}.\:{one}\:{end}\:{of}\:{the}\:{rod}\:{is}\:{hinged}.\: \\ $$$${no}\:{friction}. \\ $$$${motion}\:{beginns}\:{at}\:\theta=\mathrm{90}°\:{from}\:{rest}. \\ $$$${find}\:{the}\:{maximal}\:{velocity}\:{of}\:{the}\: \\ $$$${cube}. \\ $$
Answered by mr W last updated on 14/Apr/21
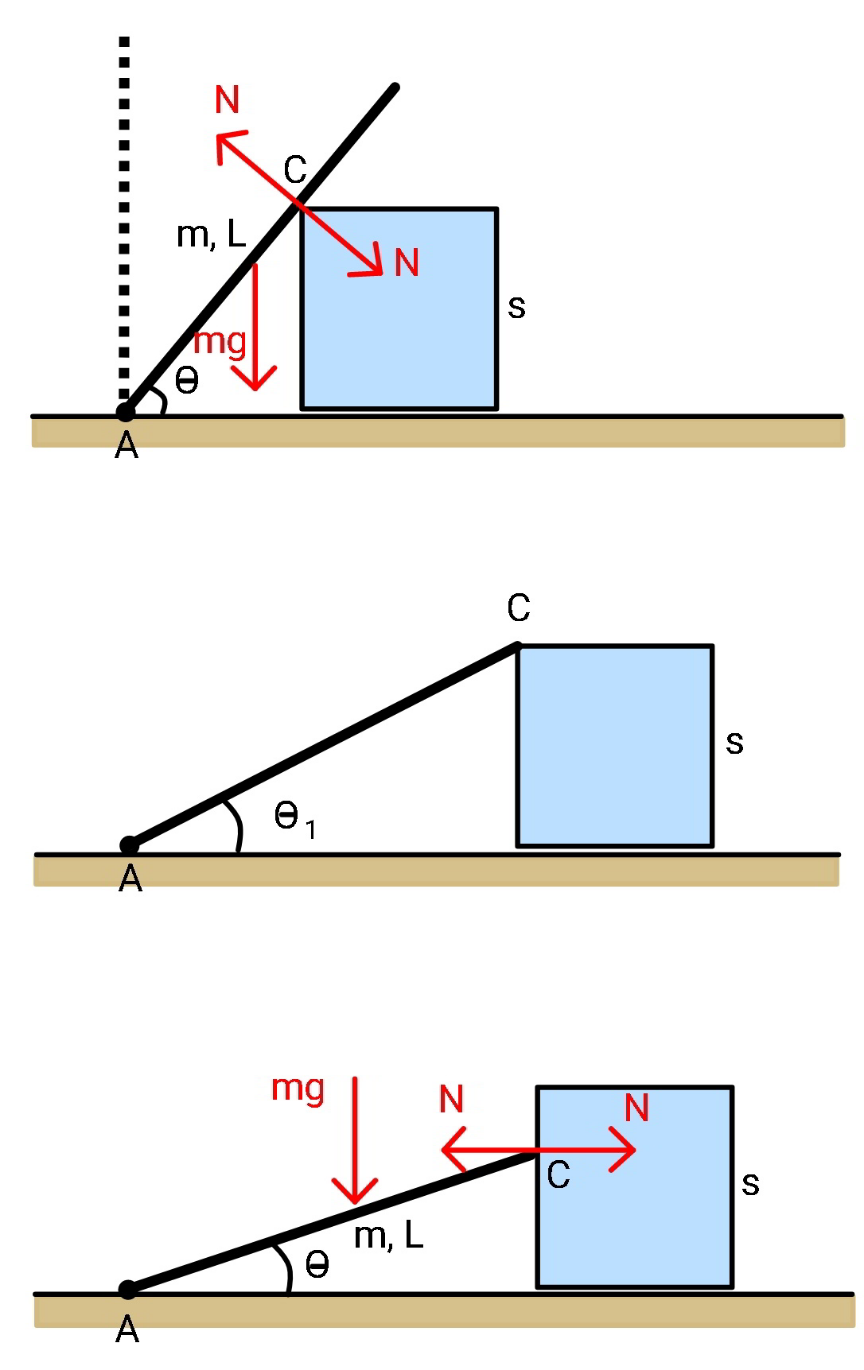
Commented by mr W last updated on 15/Apr/21
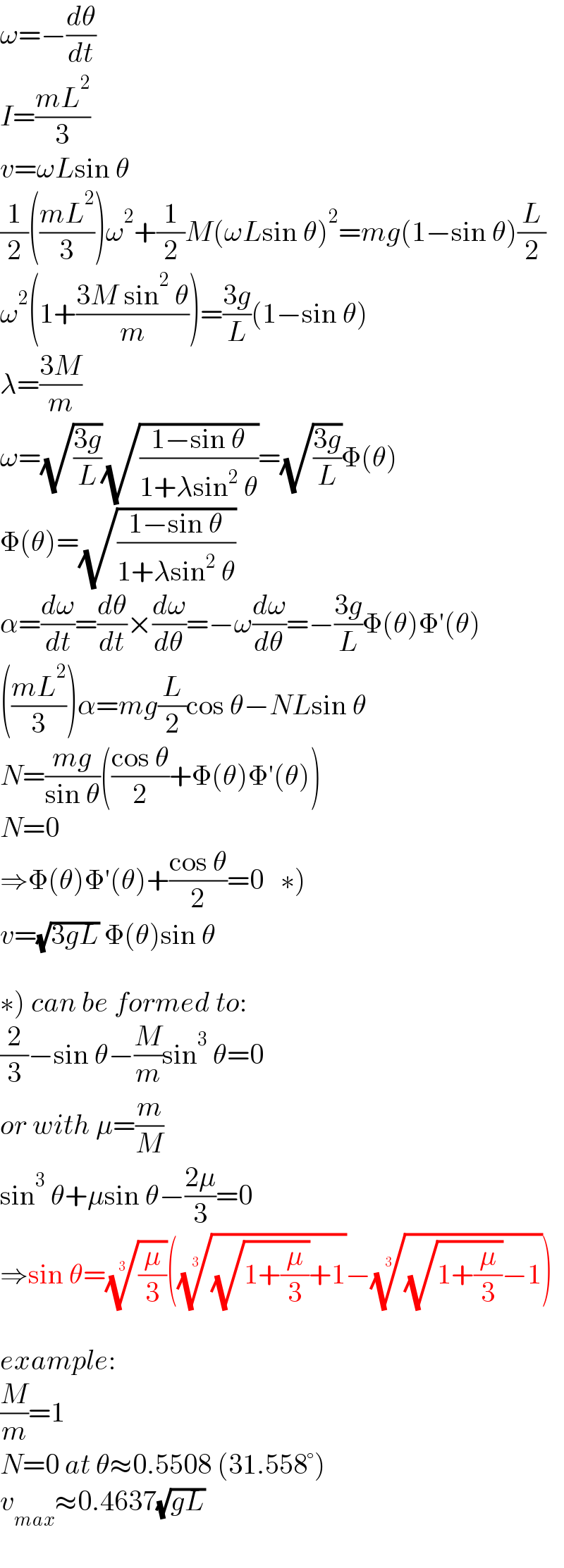
ω=−(dθ/dt) I=((mL^2 )/3) v=ωLsin θ (1/2)(((mL^2 )/3))ω^2 +(1/2)M(ωLsin θ)^2 =mg(1−sin θ)(L/2) ω^2 (1+((3M sin^2 θ)/m))=((3g)/L)(1−sin θ) λ=((3M)/m) ω=(√((3g)/L))(√((1−sin θ)/(1+λsin^2 θ)))=(√((3g)/L))Φ(θ) Φ(θ)=(√((1−sin θ)/(1+λsin^2 θ))) α=(dω/dt)=(dθ/dt)×(dω/dθ)=−ω(dω/dθ)=−((3g)/L)Φ(θ)Φ′(θ) (((mL^2 )/3))α=mg(L/2)cos θ−NLsin θ N=((mg)/(sin θ))(((cos θ)/2)+Φ(θ)Φ′(θ)) N=0 ⇒Φ(θ)Φ′(θ)+((cos θ)/2)=0 ∗) v=(√(3gL)) Φ(θ)sin θ ∗) can be formed to: (2/3)−sin θ−(M/m)sin^3 θ=0 or with μ=(m/M) sin^3 θ+μsin θ−((2μ)/3)=0 ⇒sin θ=((μ/3))^(1/3) ((((√(1+(μ/3)))+1))^(1/3) −(((√(1+(μ/3)))−1))^(1/3) ) example: (M/m)=1 N=0 at θ≈0.5508 (31.558°) v_(max) ≈0.4637(√(gL))
$$\omega=−\frac{{d}\theta}{{dt}} \\ $$$${I}=\frac{{mL}^{\mathrm{2}} }{\mathrm{3}} \\ $$$${v}=\omega{L}\mathrm{sin}\:\theta \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{mL}^{\mathrm{2}} }{\mathrm{3}}\right)\omega^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{M}\left(\omega{L}\mathrm{sin}\:\theta\right)^{\mathrm{2}} ={mg}\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\frac{{L}}{\mathrm{2}} \\ $$$$\omega^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{3}{M}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{m}}\right)=\frac{\mathrm{3}{g}}{{L}}\left(\mathrm{1}−\mathrm{sin}\:\theta\right) \\ $$$$\lambda=\frac{\mathrm{3}{M}}{{m}} \\ $$$$\omega=\sqrt{\frac{\mathrm{3}{g}}{{L}}}\sqrt{\frac{\mathrm{1}−\mathrm{sin}\:\theta}{\mathrm{1}+\lambda\mathrm{sin}^{\mathrm{2}} \:\theta}}=\sqrt{\frac{\mathrm{3}{g}}{{L}}}\Phi\left(\theta\right) \\ $$$$\Phi\left(\theta\right)=\sqrt{\frac{\mathrm{1}−\mathrm{sin}\:\theta}{\mathrm{1}+\lambda\mathrm{sin}^{\mathrm{2}} \:\theta}} \\ $$$$\alpha=\frac{{d}\omega}{{dt}}=\frac{{d}\theta}{{dt}}×\frac{{d}\omega}{{d}\theta}=−\omega\frac{{d}\omega}{{d}\theta}=−\frac{\mathrm{3}{g}}{{L}}\Phi\left(\theta\right)\Phi'\left(\theta\right) \\ $$$$\left(\frac{{mL}^{\mathrm{2}} }{\mathrm{3}}\right)\alpha={mg}\frac{{L}}{\mathrm{2}}\mathrm{cos}\:\theta−{NL}\mathrm{sin}\:\theta \\ $$$${N}=\frac{{mg}}{\mathrm{sin}\:\theta}\left(\frac{\mathrm{cos}\:\theta}{\mathrm{2}}+\Phi\left(\theta\right)\Phi'\left(\theta\right)\right) \\ $$$${N}=\mathrm{0} \\ $$$$\left.\Rightarrow\Phi\left(\theta\right)\Phi'\left(\theta\right)+\frac{\mathrm{cos}\:\theta}{\mathrm{2}}=\mathrm{0}\:\:\:\ast\right) \\ $$$${v}=\sqrt{\mathrm{3}{gL}}\:\Phi\left(\theta\right)\mathrm{sin}\:\theta \\ $$$$ \\ $$$$\left.\ast\right)\:{can}\:{be}\:{formed}\:{to}: \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{sin}\:\theta−\frac{{M}}{{m}}\mathrm{sin}^{\mathrm{3}} \:\theta=\mathrm{0} \\ $$$${or}\:{with}\:\mu=\frac{{m}}{{M}} \\ $$$$\mathrm{sin}^{\mathrm{3}} \:\theta+\mu\mathrm{sin}\:\theta−\frac{\mathrm{2}\mu}{\mathrm{3}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\sqrt[{\mathrm{3}}]{\frac{\mu}{\mathrm{3}}}\left(\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{1}+\frac{\mu}{\mathrm{3}}}+\mathrm{1}}−\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{1}+\frac{\mu}{\mathrm{3}}}−\mathrm{1}}\right) \\ $$$$ \\ $$$${example}: \\ $$$$\frac{{M}}{{m}}=\mathrm{1} \\ $$$${N}=\mathrm{0}\:{at}\:\theta\approx\mathrm{0}.\mathrm{5508}\:\left(\mathrm{31}.\mathrm{558}°\right) \\ $$$${v}_{{max}} \approx\mathrm{0}.\mathrm{4637}\sqrt{{gL}} \\ $$
Commented by ajfour last updated on 15/Apr/21
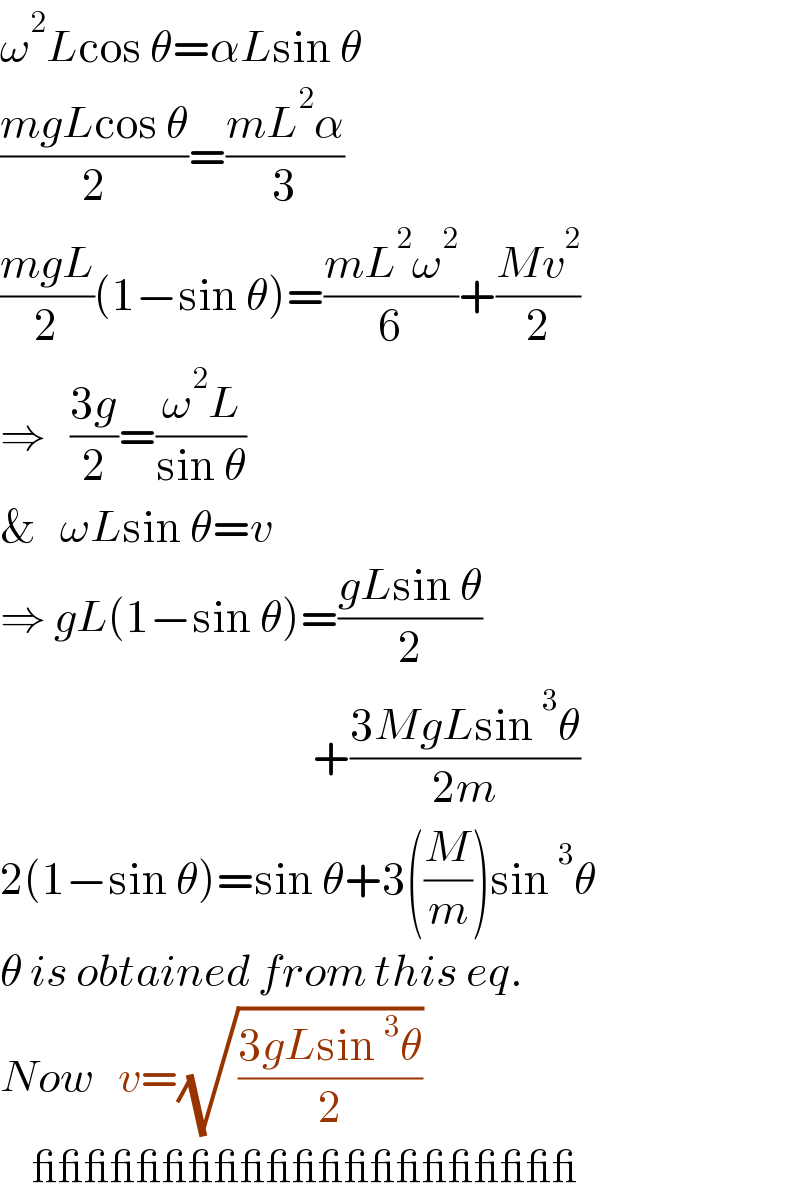
ω^2 Lcos θ=αLsin θ ((mgLcos θ)/2)=((mL^2 α)/3) ((mgL)/2)(1−sin θ)=((mL^2 ω^2 )/6)+((Mv^2 )/2) ⇒ ((3g)/2)=((ω^2 L)/(sin θ)) & ωLsin θ=v ⇒ gL(1−sin θ)=((gLsin θ)/2) +((3MgLsin^3 θ)/(2m)) 2(1−sin θ)=sin θ+3((M/m))sin^3 θ θ is obtained from this eq. Now v=(√((3gLsin^3 θ)/2)) _____________________
$$\omega^{\mathrm{2}} {L}\mathrm{cos}\:\theta=\alpha{L}\mathrm{sin}\:\theta \\ $$$$\frac{{mgL}\mathrm{cos}\:\theta}{\mathrm{2}}=\frac{{mL}^{\mathrm{2}} \alpha}{\mathrm{3}} \\ $$$$\frac{{mgL}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{sin}\:\theta\right)=\frac{{mL}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{6}}+\frac{{Mv}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\frac{\mathrm{3}{g}}{\mathrm{2}}=\frac{\omega^{\mathrm{2}} {L}}{\mathrm{sin}\:\theta} \\ $$$$\&\:\:\:\omega{L}\mathrm{sin}\:\theta={v} \\ $$$$\Rightarrow\:{gL}\left(\mathrm{1}−\mathrm{sin}\:\theta\right)=\frac{{gL}\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{\mathrm{3}{MgL}\mathrm{sin}\:^{\mathrm{3}} \theta}{\mathrm{2}{m}} \\ $$$$\mathrm{2}\left(\mathrm{1}−\mathrm{sin}\:\theta\right)=\mathrm{sin}\:\theta+\mathrm{3}\left(\frac{{M}}{{m}}\right)\mathrm{sin}\:^{\mathrm{3}} \theta \\ $$$$\theta\:{is}\:{obtained}\:{from}\:{this}\:{eq}. \\ $$$${Now}\:\:\:{v}=\sqrt{\frac{\mathrm{3}{gL}\mathrm{sin}\:^{\mathrm{3}} \theta}{\mathrm{2}}} \\ $$$$\:\:\:\:\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$
Commented by ajfour last updated on 15/Apr/21
yes sir, thanks; corrected.
$${yes}\:{sir},\:{thanks};\:{corrected}. \\ $$
Commented by mr W last updated on 15/Apr/21
nice solution sir!
$${nice}\:{solution}\:{sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *