Question Number 138386 by ajfour last updated on 13/Apr/21

Commented by ajfour last updated on 13/Apr/21
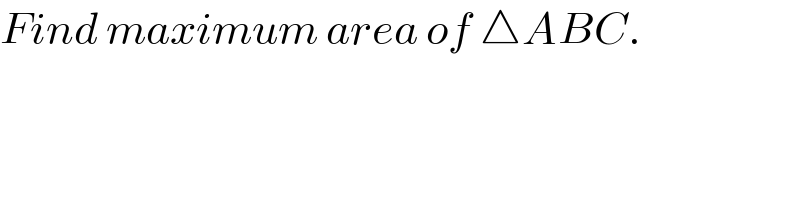
$${Find}\:{maximum}\:{area}\:{of}\:\bigtriangleup{ABC}. \\ $$
Answered by mr W last updated on 13/Apr/21

Commented by mr W last updated on 13/Apr/21

$${C}\left({c},\mathrm{0}\right)\:{with}\:\sqrt{\mathrm{3}}\leqslant{c}\leqslant\sqrt{\mathrm{15}} \\ $$$${D}\left({c},\mathrm{1}\right) \\ $$$${say}\:{E}\left({h},{k}\right) \\ $$$${h}^{\mathrm{2}} +{k}^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} =\mathrm{4}\:\:\:…\left({i}\right) \\ $$$$\left({h}−{c}\right)^{\mathrm{2}} +\left({k}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} =\mathrm{4}\:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$${c}\left(\mathrm{2}{h}−{c}\right)+\left(\mathrm{2}{k}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{h}=\frac{{c}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{k}}{\mathrm{2}{c}} \\ $$$$\left(\frac{{c}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{k}}{\mathrm{2}{c}}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} =\mathrm{4} \\ $$$${k}^{\mathrm{2}} −{k}+\frac{{c}^{\mathrm{2}} +\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{4}{c}^{\mathrm{2}} }{{c}^{\mathrm{2}} +\mathrm{1}}=\mathrm{0} \\ $$$${k}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{c}\sqrt{\frac{\mathrm{15}−{c}^{\mathrm{2}} }{{c}^{\mathrm{2}} +\mathrm{1}}}\right) \\ $$$${y}_{{B}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{k}\right)=\frac{\mathrm{3}}{\mathrm{4}}+\frac{{c}}{\mathrm{4}}\sqrt{\frac{\mathrm{15}−{c}^{\mathrm{2}} }{{c}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\Delta_{{ABC}} ={A}=\frac{{cy}_{{B}} }{\mathrm{2}} \\ $$$$\Rightarrow{A}=\frac{{c}}{\mathrm{8}}\left(\mathrm{3}+{c}\sqrt{\frac{\mathrm{15}−{c}^{\mathrm{2}} }{{c}^{\mathrm{2}} +\mathrm{1}}}\right) \\ $$$${for}\:{A}_{{max}} :\:\frac{{dA}}{{dc}}=\mathrm{0} \\ $$$${A}_{{max}} \approx\mathrm{2}.\mathrm{0378}\:{when}\:{c}\approx\mathrm{3}.\mathrm{2959} \\ $$
Commented by mr W last updated on 13/Apr/21

Commented by ajfour last updated on 13/Apr/21

$${Thank}\:{you}\:{sir},\:{your}\:{way}\:{is} \\ $$$${fine}\:{enough}! \\ $$
