Question Number 138485 by SLVR last updated on 14/Apr/21
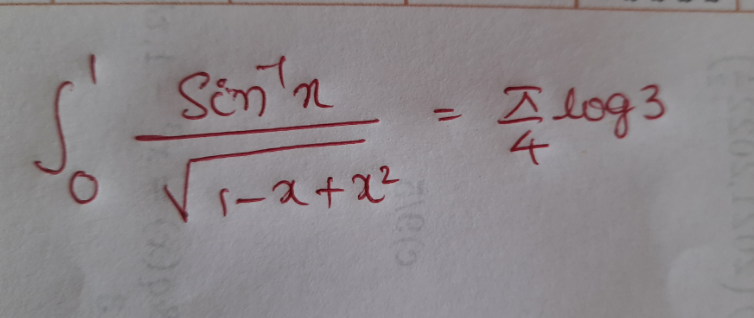
Commented by SLVR last updated on 14/Apr/21
$${Good}\:{morning}\:{mr}.{W}\:{thanks}\:{for} \\ $$$${your}\:{support}\:.{The}\:{above}\:{is}\:{also}\:{i} \\ $$$${missed}\:{long}\:{ago}..{and}\:{i}\:{couldnot} \\ $$$${retrive}\:{from}\:{the}\:{group}.{kindly}\:{help} \\ $$
Answered by phanphuoc last updated on 14/Apr/21
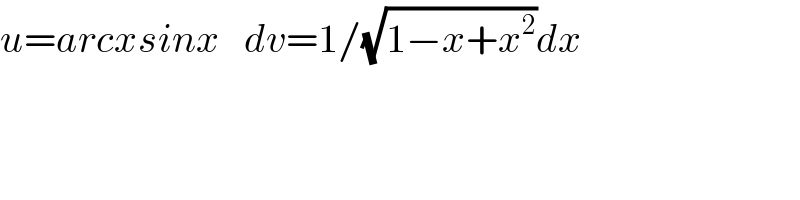
$${u}={arcxsinx}\:\:\:{dv}=\mathrm{1}/\sqrt{\mathrm{1}−{x}+{x}^{\mathrm{2}} }{dx} \\ $$
Answered by Ñï= last updated on 14/Apr/21

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{si}{n}^{−\mathrm{1}} \sqrt{{x}}}{\:\sqrt{\mathrm{1}−{x}+{x}^{\mathrm{2}} }}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{sin}^{−\mathrm{1}} \sqrt{\mathrm{1}−{x}}}{\:\sqrt{\mathrm{1}−{x}+{x}^{\mathrm{2}} }}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}} \\ $$$$=\frac{\pi}{\mathrm{4}}{ln}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{1}−{x}+{x}^{\mathrm{2}} }\right)_{\mathrm{0}} ^{\mathrm{1}} =\frac{\pi}{\mathrm{4}}{ln}\:\mathrm{3} \\ $$$$\left\{\mathrm{sin}^{−\mathrm{1}} \sqrt{{x}}+\mathrm{sin}^{−\mathrm{1}} \sqrt{\mathrm{1}−{x}}=\frac{\pi}{\mathrm{2}},\int\frac{{du}}{\:\sqrt{{u}^{\mathrm{2}} +{a}^{\mathrm{2}} }}={ln}\mid{u}+\sqrt{{u}^{\mathrm{2}} +{a}^{\mathrm{2}} }\mid+{C}\right\} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{sin}^{−\mathrm{1}} {x}}{\:\sqrt{\mathrm{1}−{x}+{x}^{\mathrm{2}} }}{dx}\cancel{=}\frac{\pi}{\mathrm{4}}{ln}\:\mathrm{3} \\ $$
Commented by SLVR last updated on 14/Apr/21

$${thanks}\:{sir}…\:{i}\:{am}\:{wrong}\:{writing} \\ $$$${the}\:{question}. \\ $$
