Menu Close

Question-138546

Tinku Tara 0 Comments
Pin




Question Number 138546 by mnjuly1970 last updated on 14/Apr/21
Answered by ajfour last updated on 14/Apr/21
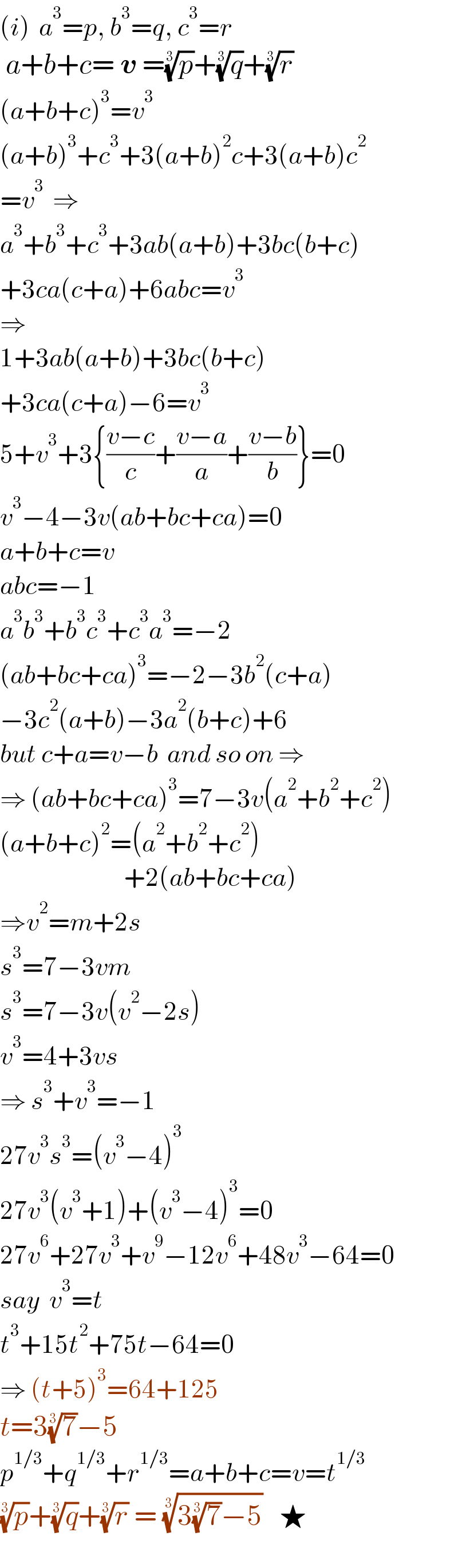
(i) a^3 =p, b^3 =q, c^3 =r a+b+c= v =(p)^(1/3) +(q)^(1/3) +(r)^(1/3) (a+b+c)^3 =v^3 (a+b)^3 +c^3 +3(a+b)^2 c+3(a+b)c^2 =v^3 ⇒ a^3 +b^3 +c^3 +3ab(a+b)+3bc(b+c) +3ca(c+a)+6abc=v^3 ⇒ 1+3ab(a+b)+3bc(b+c) +3ca(c+a)−6=v^3 5+v^3 +3{((v−c)/c)+((v−a)/a)+((v−b)/b)}=0 v^3 −4−3v(ab+bc+ca)=0 a+b+c=v abc=−1 a^3 b^3 +b^3 c^3 +c^3 a^3 =−2 (ab+bc+ca)^3 =−2−3b^2 (c+a) −3c^2 (a+b)−3a^2 (b+c)+6 but c+a=v−b and so on ⇒ ⇒ (ab+bc+ca)^3 =7−3v(a^2 +b^2 +c^2 ) (a+b+c)^2 =(a^2 +b^2 +c^2 ) +2(ab+bc+ca) ⇒v^2 =m+2s s^3 =7−3vm s^3 =7−3v(v^2 −2s) v^3 =4+3vs ⇒ s^3 +v^3 =−1 27v^3 s^3 =(v^3 −4)^3 27v^3 (v^3 +1)+(v^3 −4)^3 =0 27v^6 +27v^3 +v^9 −12v^6 +48v^3 −64=0 say v^3 =t t^3 +15t^2 +75t−64=0 ⇒ (t+5)^3 =64+125 t=3(7)^(1/3) −5 p^(1/3) +q^(1/3) +r^(1/3) =a+b+c=v=t^(1/3) (p)^(1/3) +(q)^(1/3) +(r)^(1/3) = ((3(7)^(1/3) −5))^(1/3) ★
$$\left({i}\right)\:\:{a}^{\mathrm{3}} ={p},\:{b}^{\mathrm{3}} ={q},\:{c}^{\mathrm{3}} ={r} \\ $$$$\:{a}+{b}+{c}=\:\boldsymbol{{v}}\:=\sqrt[{\mathrm{3}}]{{p}}+\sqrt[{\mathrm{3}}]{{q}}+\sqrt[{\mathrm{3}}]{{r}} \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{3}} ={v}^{\mathrm{3}} \\ $$$$\left({a}+{b}\right)^{\mathrm{3}} +{c}^{\mathrm{3}} +\mathrm{3}\left({a}+{b}\right)^{\mathrm{2}} {c}+\mathrm{3}\left({a}+{b}\right){c}^{\mathrm{2}} \\ $$$$={v}^{\mathrm{3}} \:\:\Rightarrow \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} +\mathrm{3}{ab}\left({a}+{b}\right)+\mathrm{3}{bc}\left({b}+{c}\right) \\ $$$$+\mathrm{3}{ca}\left({c}+{a}\right)+\mathrm{6}{abc}={v}^{\mathrm{3}} \\ $$$$\Rightarrow \\ $$$$\mathrm{1}+\mathrm{3}{ab}\left({a}+{b}\right)+\mathrm{3}{bc}\left({b}+{c}\right) \\ $$$$+\mathrm{3}{ca}\left({c}+{a}\right)−\mathrm{6}={v}^{\mathrm{3}} \\ $$$$\mathrm{5}+{v}^{\mathrm{3}} +\mathrm{3}\left\{\frac{{v}−{c}}{{c}}+\frac{{v}−{a}}{{a}}+\frac{{v}−{b}}{{b}}\right\}=\mathrm{0} \\ $$$${v}^{\mathrm{3}} −\mathrm{4}−\mathrm{3}{v}\left({ab}+{bc}+{ca}\right)=\mathrm{0} \\ $$$${a}+{b}+{c}={v} \\ $$$${abc}=−\mathrm{1} \\ $$$${a}^{\mathrm{3}} {b}^{\mathrm{3}} +{b}^{\mathrm{3}} {c}^{\mathrm{3}} +{c}^{\mathrm{3}} {a}^{\mathrm{3}} =−\mathrm{2} \\ $$$$\left({ab}+{bc}+{ca}\right)^{\mathrm{3}} =−\mathrm{2}−\mathrm{3}{b}^{\mathrm{2}} \left({c}+{a}\right) \\ $$$$−\mathrm{3}{c}^{\mathrm{2}} \left({a}+{b}\right)−\mathrm{3}{a}^{\mathrm{2}} \left({b}+{c}\right)+\mathrm{6} \\ $$$${but}\:{c}+{a}={v}−{b}\:\:{and}\:{so}\:{on}\:\Rightarrow \\ $$$$\Rightarrow\:\left({ab}+{bc}+{ca}\right)^{\mathrm{3}} =\mathrm{7}−\mathrm{3}{v}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{2}} =\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}\left({ab}+{bc}+{ca}\right) \\ $$$$\Rightarrow{v}^{\mathrm{2}} ={m}+\mathrm{2}{s} \\ $$$${s}^{\mathrm{3}} =\mathrm{7}−\mathrm{3}{vm} \\ $$$${s}^{\mathrm{3}} =\mathrm{7}−\mathrm{3}{v}\left({v}^{\mathrm{2}} −\mathrm{2}{s}\right) \\ $$$${v}^{\mathrm{3}} =\mathrm{4}+\mathrm{3}{vs} \\ $$$$\Rightarrow\:{s}^{\mathrm{3}} +{v}^{\mathrm{3}} =−\mathrm{1} \\ $$$$\mathrm{27}{v}^{\mathrm{3}} {s}^{\mathrm{3}} =\left({v}^{\mathrm{3}} −\mathrm{4}\right)^{\mathrm{3}} \\ $$$$\mathrm{27}{v}^{\mathrm{3}} \left({v}^{\mathrm{3}} +\mathrm{1}\right)+\left({v}^{\mathrm{3}} −\mathrm{4}\right)^{\mathrm{3}} =\mathrm{0} \\ $$$$\mathrm{27}{v}^{\mathrm{6}} +\mathrm{27}{v}^{\mathrm{3}} +{v}^{\mathrm{9}} −\mathrm{12}{v}^{\mathrm{6}} +\mathrm{48}{v}^{\mathrm{3}} −\mathrm{64}=\mathrm{0} \\ $$$${say}\:\:{v}^{\mathrm{3}} ={t} \\ $$$${t}^{\mathrm{3}} +\mathrm{15}{t}^{\mathrm{2}} +\mathrm{75}{t}−\mathrm{64}=\mathrm{0} \\ $$$$\Rightarrow\:\left({t}+\mathrm{5}\right)^{\mathrm{3}} =\mathrm{64}+\mathrm{125} \\ $$$${t}=\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{7}}−\mathrm{5} \\ $$$${p}^{\mathrm{1}/\mathrm{3}} +{q}^{\mathrm{1}/\mathrm{3}} +{r}^{\mathrm{1}/\mathrm{3}} ={a}+{b}+{c}={v}={t}^{\mathrm{1}/\mathrm{3}} \\ $$$$\sqrt[{\mathrm{3}}]{{p}}+\sqrt[{\mathrm{3}}]{{q}}+\sqrt[{\mathrm{3}}]{{r}}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{7}}−\mathrm{5}}\:\:\:\bigstar \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 14/Apr/21
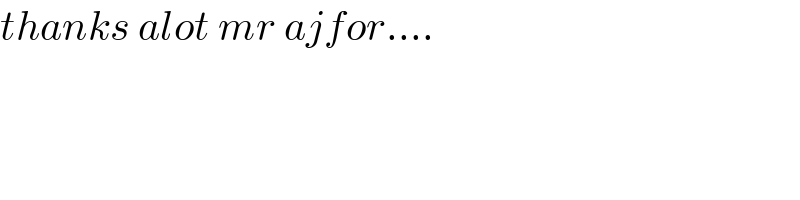
thanks alot mr ajfor....
$${thanks}\:{alot}\:{mr}\:{ajfor}…. \\ $$
Commented by ajfour last updated on 14/Apr/21
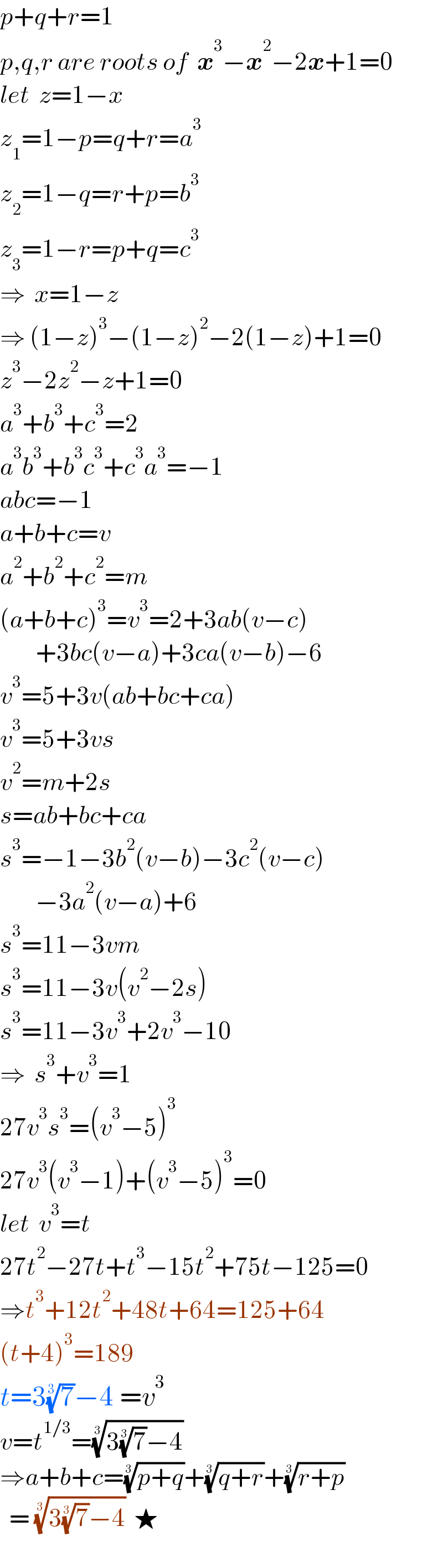
p+q+r=1 p,q,r are roots of x^3 −x^2 −2x+1=0 let z=1−x z_1 =1−p=q+r=a^3 z_2 =1−q=r+p=b^3 z_3 =1−r=p+q=c^3 ⇒ x=1−z ⇒ (1−z)^3 −(1−z)^2 −2(1−z)+1=0 z^3 −2z^2 −z+1=0 a^3 +b^3 +c^3 =2 a^3 b^3 +b^3 c^3 +c^3 a^3 =−1 abc=−1 a+b+c=v a^2 +b^2 +c^2 =m (a+b+c)^3 =v^3 =2+3ab(v−c) +3bc(v−a)+3ca(v−b)−6 v^3 =5+3v(ab+bc+ca) v^3 =5+3vs v^2 =m+2s s=ab+bc+ca s^3 =−1−3b^2 (v−b)−3c^2 (v−c) −3a^2 (v−a)+6 s^3 =11−3vm s^3 =11−3v(v^2 −2s) s^3 =11−3v^3 +2v^3 −10 ⇒ s^3 +v^3 =1 27v^3 s^3 =(v^3 −5)^3 27v^3 (v^3 −1)+(v^3 −5)^3 =0 let v^3 =t 27t^2 −27t+t^3 −15t^2 +75t−125=0 ⇒t^3 +12t^2 +48t+64=125+64 (t+4)^3 =189 t=3(7)^(1/3) −4 =v^3 v=t^(1/3) =((3(7)^(1/3) −4))^(1/3) ⇒a+b+c=((p+q))^(1/3) +((q+r))^(1/3) +((r+p))^(1/3) = ((3(7)^(1/3) −4))^(1/3) ★
$${p}+{q}+{r}=\mathrm{1} \\ $$$${p},{q},{r}\:{are}\:{roots}\:{of}\:\:\boldsymbol{{x}}^{\mathrm{3}} −\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{x}}+\mathrm{1}=\mathrm{0} \\ $$$${let}\:\:{z}=\mathrm{1}−{x} \\ $$$${z}_{\mathrm{1}} =\mathrm{1}−{p}={q}+{r}={a}^{\mathrm{3}} \\ $$$${z}_{\mathrm{2}} =\mathrm{1}−{q}={r}+{p}={b}^{\mathrm{3}} \\ $$$${z}_{\mathrm{3}} =\mathrm{1}−{r}={p}+{q}={c}^{\mathrm{3}} \\ $$$$\Rightarrow\:\:{x}=\mathrm{1}−{z} \\ $$$$\Rightarrow\:\left(\mathrm{1}−{z}\right)^{\mathrm{3}} −\left(\mathrm{1}−{z}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}−{z}\right)+\mathrm{1}=\mathrm{0} \\ $$$${z}^{\mathrm{3}} −\mathrm{2}{z}^{\mathrm{2}} −{z}+\mathrm{1}=\mathrm{0} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\mathrm{2} \\ $$$${a}^{\mathrm{3}} {b}^{\mathrm{3}} +{b}^{\mathrm{3}} {c}^{\mathrm{3}} +{c}^{\mathrm{3}} {a}^{\mathrm{3}} =−\mathrm{1} \\ $$$${abc}=−\mathrm{1} \\ $$$${a}+{b}+{c}={v} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} ={m} \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{3}} ={v}^{\mathrm{3}} =\mathrm{2}+\mathrm{3}{ab}\left({v}−{c}\right) \\ $$$$\:\:\:\:\:\:\:\:+\mathrm{3}{bc}\left({v}−{a}\right)+\mathrm{3}{ca}\left({v}−{b}\right)−\mathrm{6} \\ $$$${v}^{\mathrm{3}} =\mathrm{5}+\mathrm{3}{v}\left({ab}+{bc}+{ca}\right) \\ $$$${v}^{\mathrm{3}} =\mathrm{5}+\mathrm{3}{vs} \\ $$$${v}^{\mathrm{2}} ={m}+\mathrm{2}{s} \\ $$$${s}={ab}+{bc}+{ca} \\ $$$${s}^{\mathrm{3}} =−\mathrm{1}−\mathrm{3}{b}^{\mathrm{2}} \left({v}−{b}\right)−\mathrm{3}{c}^{\mathrm{2}} \left({v}−{c}\right) \\ $$$$\:\:\:\:\:\:\:\:−\mathrm{3}{a}^{\mathrm{2}} \left({v}−{a}\right)+\mathrm{6} \\ $$$${s}^{\mathrm{3}} =\mathrm{11}−\mathrm{3}{vm} \\ $$$${s}^{\mathrm{3}} =\mathrm{11}−\mathrm{3}{v}\left({v}^{\mathrm{2}} −\mathrm{2}{s}\right) \\ $$$${s}^{\mathrm{3}} =\mathrm{11}−\mathrm{3}{v}^{\mathrm{3}} +\mathrm{2}{v}^{\mathrm{3}} −\mathrm{10} \\ $$$$\Rightarrow\:\:{s}^{\mathrm{3}} +{v}^{\mathrm{3}} =\mathrm{1} \\ $$$$\mathrm{27}{v}^{\mathrm{3}} {s}^{\mathrm{3}} =\left({v}^{\mathrm{3}} −\mathrm{5}\right)^{\mathrm{3}} \\ $$$$\mathrm{27}{v}^{\mathrm{3}} \left({v}^{\mathrm{3}} −\mathrm{1}\right)+\left({v}^{\mathrm{3}} −\mathrm{5}\right)^{\mathrm{3}} =\mathrm{0} \\ $$$${let}\:\:{v}^{\mathrm{3}} ={t} \\ $$$$\mathrm{27}{t}^{\mathrm{2}} −\mathrm{27}{t}+{t}^{\mathrm{3}} −\mathrm{15}{t}^{\mathrm{2}} +\mathrm{75}{t}−\mathrm{125}=\mathrm{0} \\ $$$$\Rightarrow{t}^{\mathrm{3}} +\mathrm{12}{t}^{\mathrm{2}} +\mathrm{48}{t}+\mathrm{64}=\mathrm{125}+\mathrm{64} \\ $$$$\left({t}+\mathrm{4}\right)^{\mathrm{3}} =\mathrm{189} \\ $$$${t}=\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{7}}−\mathrm{4}\:={v}^{\mathrm{3}} \\ $$$${v}={t}^{\mathrm{1}/\mathrm{3}} =\sqrt[{\mathrm{3}}]{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{7}}−\mathrm{4}} \\ $$$$\Rightarrow{a}+{b}+{c}=\sqrt[{\mathrm{3}}]{{p}+{q}}+\sqrt[{\mathrm{3}}]{{q}+{r}}+\sqrt[{\mathrm{3}}]{{r}+{p}} \\ $$$$\:\:=\:\sqrt[{\mathrm{3}}]{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{7}}−\mathrm{4}}\:\:\bigstar \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 14/Apr/21
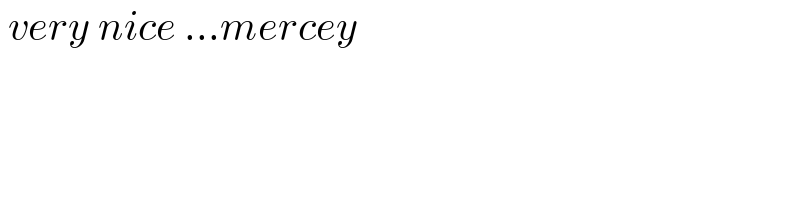
very nice ...mercey
$$\:{very}\:{nice}\:…{mercey} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *