Question Number 138658 by ajfour last updated on 16/Apr/21
Commented by ajfour last updated on 16/Apr/21
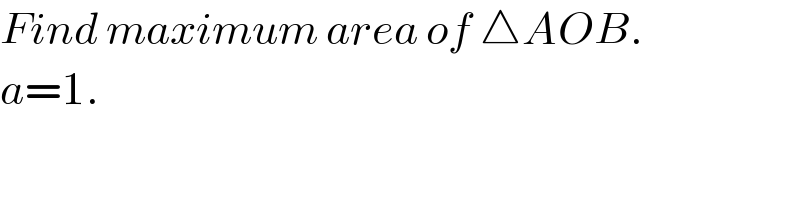
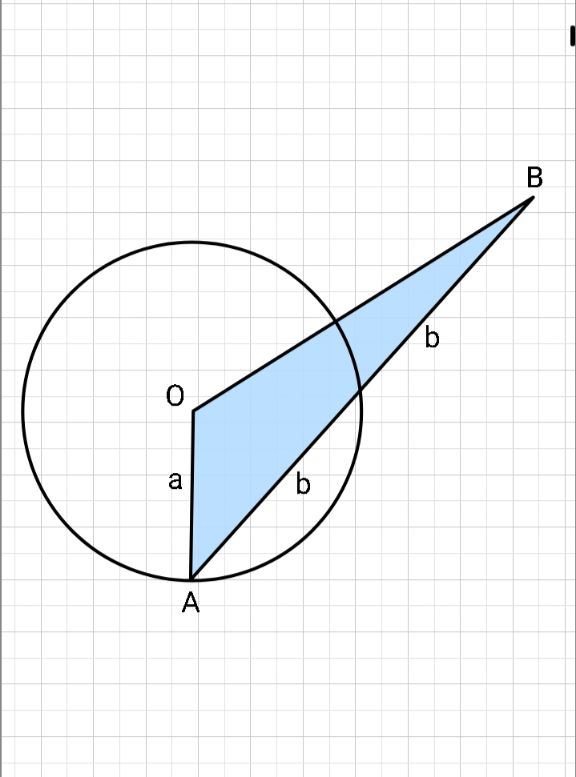
$${Find}\:{maximum}\:{area}\:{of}\:\bigtriangleup{AOB}. \\ $$$${a}=\mathrm{1}. \\ $$
Commented by mr W last updated on 16/Apr/21
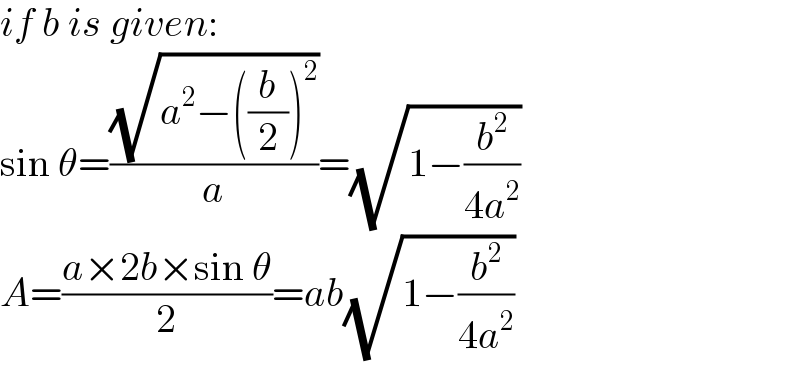
$${if}\:{b}\:{is}\:{given}: \\ $$$$\mathrm{sin}\:\theta=\frac{\sqrt{{a}^{\mathrm{2}} −\left(\frac{{b}}{\mathrm{2}}\right)^{\mathrm{2}} }}{{a}}=\sqrt{\mathrm{1}−\frac{{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }} \\ $$$${A}=\frac{{a}×\mathrm{2}{b}×\mathrm{sin}\:\theta}{\mathrm{2}}={ab}\sqrt{\mathrm{1}−\frac{{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }} \\ $$
Answered by ajfour last updated on 16/Apr/21
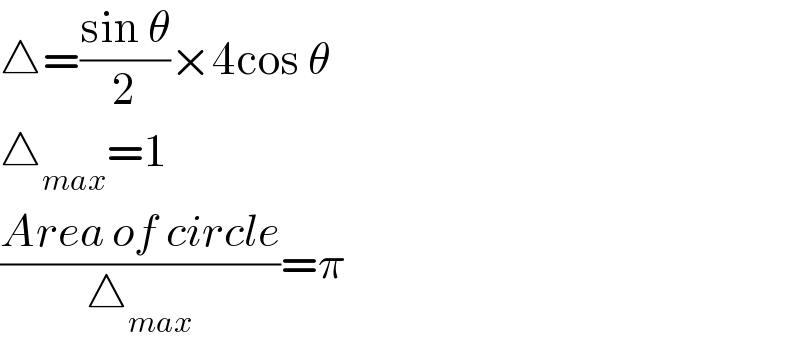
$$\bigtriangleup=\frac{\mathrm{sin}\:\theta}{\mathrm{2}}×\mathrm{4cos}\:\theta \\ $$$$\bigtriangleup_{{max}} =\mathrm{1} \\ $$$$\frac{{Area}\:{of}\:{circle}}{\bigtriangleup_{{max}} }=\pi \\ $$
