Question Number 138774 by Bekzod Jumayev last updated on 18/Apr/21

Commented by Bekzod Jumayev last updated on 18/Apr/21

$$\:\:\:\:\:\:\boldsymbol{{x}}=?? \\ $$$$\boldsymbol{{Please}}\:\boldsymbol{{help}} \\ $$
Answered by nimnim last updated on 18/Apr/21

$$\:\:{If}\:{AG}//{BF},\:{then} \\ $$$$\angle{BFA}=\angle{GAF}=\mathrm{2}\theta\:\left({alt}.\:{int}.\angle'{s},\:{as}\:{AG}\parallel{BF}\right) \\ $$$${in}\:{rt}.\bigtriangleup{CEF},\:\angle{ECF}+\angle{EFC}=\mathrm{90}° \\ $$$$\:\:\:\:\:\:\Rightarrow\:\mathrm{4}\theta+\mathrm{2}\theta=\mathrm{90}\Rightarrow\theta=\mathrm{15}° \\ $$$${in}\:{rt}.\:\bigtriangleup{ECD},\:{CD}\:{is}\:{produced}\:{to}\:{H} \\ $$$$\:\:\therefore\:\angle{EDH}=\mathrm{90}+\mathrm{2}\theta \\ $$$$\:\:\Rightarrow\angle{ADH}=\mathrm{90}+\mathrm{2}\theta \\ $$$${in}\:\bigtriangleup{ADH},\:{AH}\:{is}\:{produced}\:{to}\:{form}\:{ext}.\angle{x} \\ $$$$\:\:\therefore\:{x}=\angle{ADH}+\angle{DAH} \\ $$$$\:\:\Rightarrow{x}=\mathrm{90}+\mathrm{2}\theta+\theta=\mathrm{90}+\mathrm{3}\left(\mathrm{15}\right)=\mathrm{135}° \\ $$
Commented by mr W last updated on 18/Apr/21
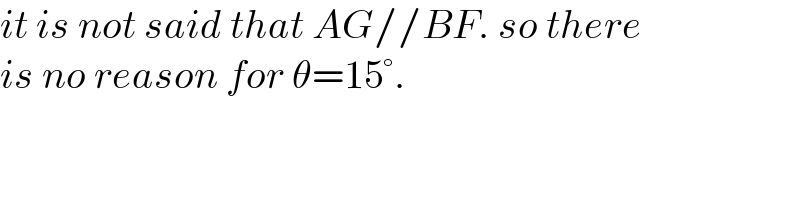
$${it}\:{is}\:{not}\:{said}\:{that}\:{AG}//{BF}.\:{so}\:{there} \\ $$$${is}\:{no}\:{reason}\:{for}\:\theta=\mathrm{15}°. \\ $$
Commented by nimnim last updated on 18/Apr/21
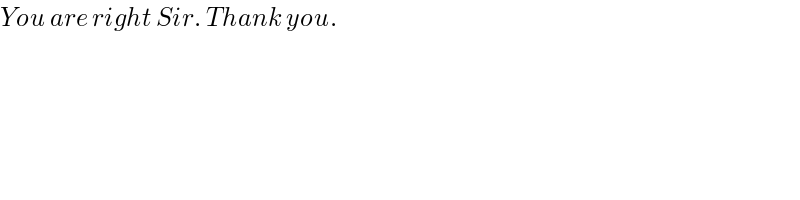
$${You}\:{are}\:{right}\:{Sir}.\:{Thank}\:{you}. \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 18/Apr/21
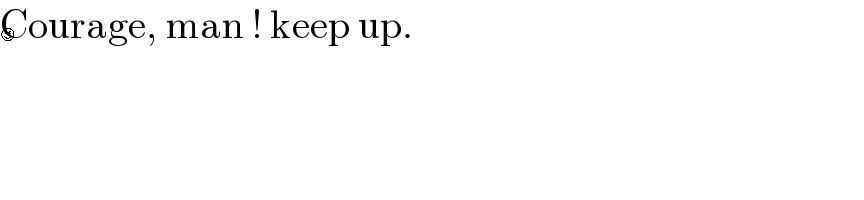
$$\mathrm{Courage},\:\mathrm{man}\:!\:\mathrm{keep}\:\mathrm{up}. \\ $$😉
