Question-138959

Question Number 138959 by mathlove last updated on 20/Apr/21

Answered by mathmax by abdo last updated on 20/Apr/21

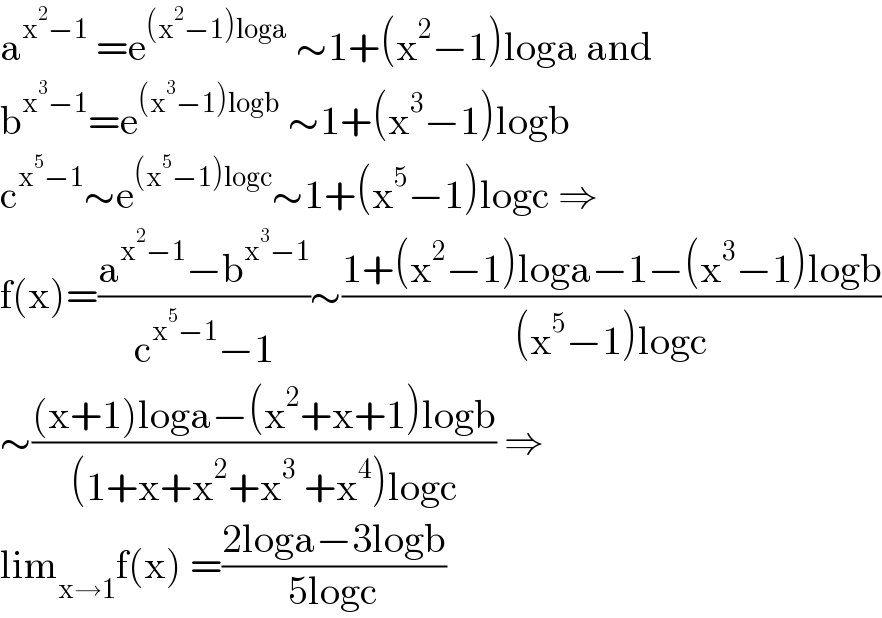
a^(x^2 −1) =e^((x^2 −1)loga) ∼1+(x^2 −1)loga and b^(x^3 −1) =e^((x^3 −1)logb) ∼1+(x^3 −1)logb c^(x^5 −1) ∼e^((x^5 −1)logc) ∼1+(x^5 −1)logc ⇒ f(x)=((a^(x^2 −1) −b^(x^3 −1) )/(c^(x^5 −1) −1))∼((1+(x^2 −1)loga−1−(x^3 −1)logb)/((x^5 −1)logc)) ∼(((x+1)loga−(x^2 +x+1)logb)/((1+x+x^2 +x^3 +x^4 )logc)) ⇒ lim_(x→1) f(x) =((2loga−3logb)/(5logc))

$$\mathrm{a}^{\mathrm{x}^{\mathrm{2}} −\mathrm{1}} \:=\mathrm{e}^{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{loga}} \:\sim\mathrm{1}+\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{loga}\:\mathrm{and} \\ $$$$\mathrm{b}^{\mathrm{x}^{\mathrm{3}} −\mathrm{1}} =\mathrm{e}^{\left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)\mathrm{logb}} \:\sim\mathrm{1}+\left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)\mathrm{logb} \\ $$$$\mathrm{c}^{\mathrm{x}^{\mathrm{5}} −\mathrm{1}} \sim\mathrm{e}^{\left(\mathrm{x}^{\mathrm{5}} −\mathrm{1}\right)\mathrm{logc}} \sim\mathrm{1}+\left(\mathrm{x}^{\mathrm{5}} −\mathrm{1}\right)\mathrm{logc}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{a}^{\mathrm{x}^{\mathrm{2}} −\mathrm{1}} −\mathrm{b}^{\mathrm{x}^{\mathrm{3}} −\mathrm{1}} }{\mathrm{c}^{\mathrm{x}^{\mathrm{5}} −\mathrm{1}} −\mathrm{1}}\sim\frac{\mathrm{1}+\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{loga}−\mathrm{1}−\left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)\mathrm{logb}}{\left(\mathrm{x}^{\mathrm{5}} −\mathrm{1}\right)\mathrm{logc}} \\ $$$$\sim\frac{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{loga}−\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)\mathrm{logb}}{\left(\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{\mathrm{3}} \:+\mathrm{x}^{\mathrm{4}} \right)\mathrm{logc}}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{2loga}−\mathrm{3logb}}{\mathrm{5logc}} \\ $$

Answered by mitica last updated on 21/Apr/21

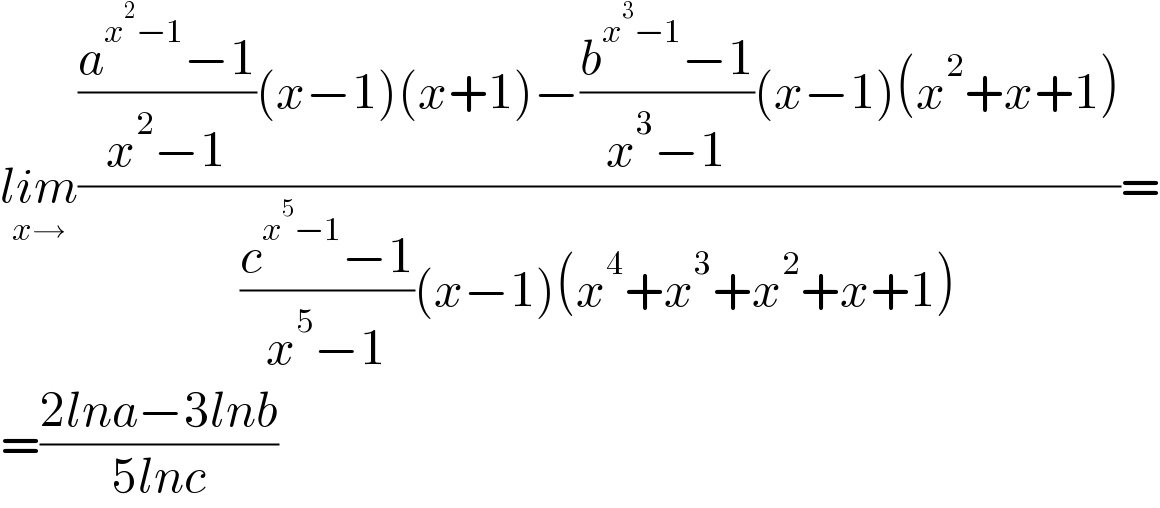
lim_(x→) ((((a^(x^2 −1) −1)/(x^2 −1))(x−1)(x+1)−((b^(x^3 −1) −1)/(x^3 −1))(x−1)(x^2 +x+1))/(((c^(x^5 −1) −1)/(x^5 −1))(x−1)(x^4 +x^3 +x^2 +x+1)))= =((2lna−3lnb)/(5lnc))

$$\underset{{x}\rightarrow} {{lim}}\frac{\frac{{a}^{{x}^{\mathrm{2}} −\mathrm{1}} −\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)−\frac{{b}^{{x}^{\mathrm{3}} −\mathrm{1}} −\mathrm{1}}{{x}^{\mathrm{3}} −\mathrm{1}}\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}{\frac{{c}^{{x}^{\mathrm{5}} −\mathrm{1}} −\mathrm{1}}{{x}^{\mathrm{5}} −\mathrm{1}}\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}= \\ $$$$=\frac{\mathrm{2}{lna}−\mathrm{3}{lnb}}{\mathrm{5}{lnc}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply