Menu Close

Question-139013

Tinku Tara 0 Comments
Pin




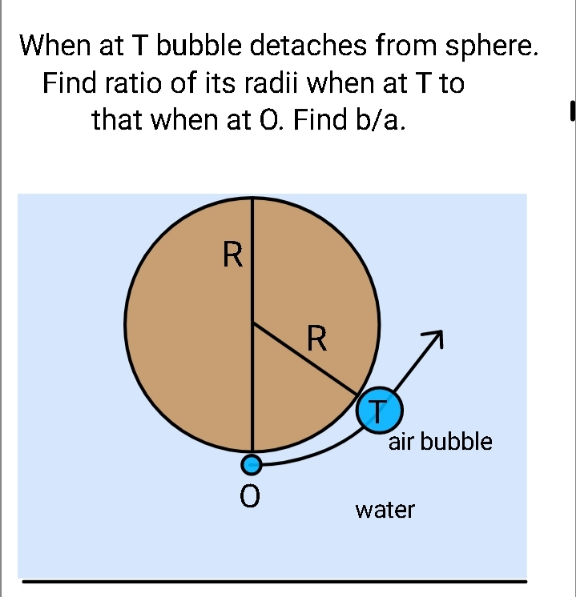
Question Number 139013 by ajfour last updated on 21/Apr/21
Answered by mr W last updated on 21/Apr/21
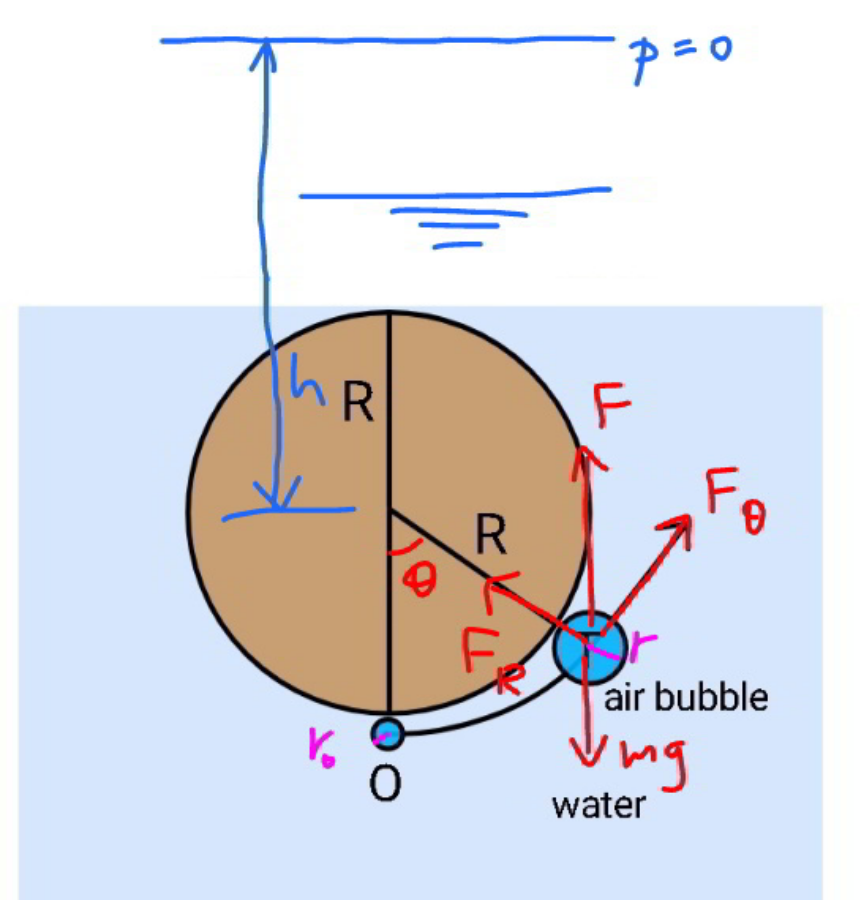
Commented by mr W last updated on 21/Apr/21
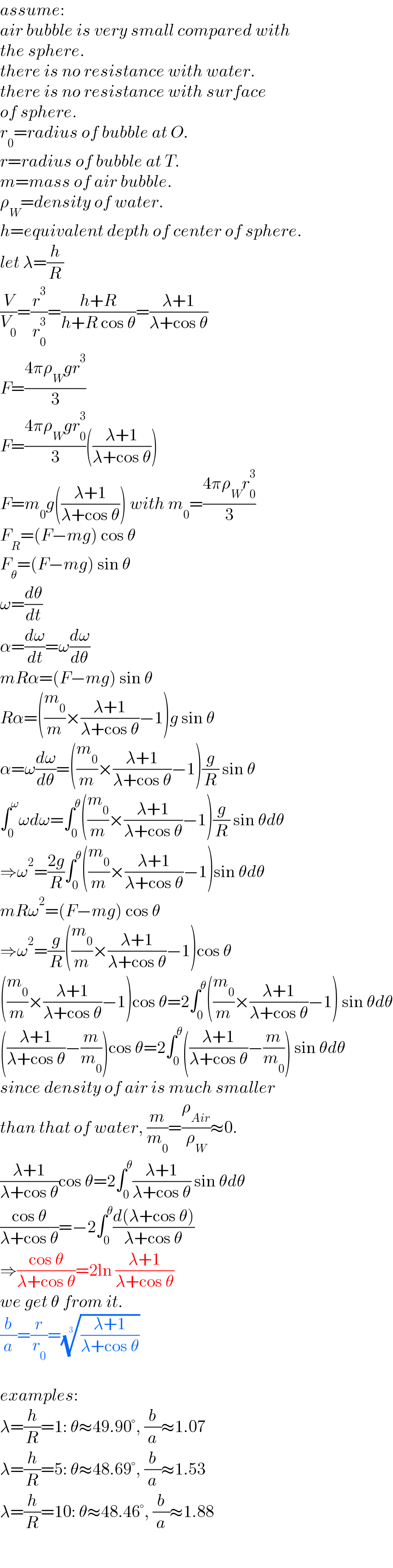
assume: air bubble is very small compared with the sphere. there is no resistance with water. there is no resistance with surface of sphere. r_0 =radius of bubble at O. r=radius of bubble at T. m=mass of air bubble. ρ_W =density of water. h=equivalent depth of center of sphere. let λ=(h/R) (V/V_0 )=(r^3 /r_0 ^3 )=((h+R)/(h+R cos θ))=((λ+1)/(λ+cos θ)) F=((4πρ_W gr^3 )/3) F=((4πρ_W gr_0 ^3 )/3)(((λ+1)/(λ+cos θ))) F=m_0 g(((λ+1)/(λ+cos θ))) with m_0 =((4πρ_W r_0 ^3 )/3) F_R =(F−mg) cos θ F_θ =(F−mg) sin θ ω=(dθ/dt) α=(dω/dt)=ω(dω/dθ) mRα=(F−mg) sin θ Rα=((m_0 /m)×((λ+1)/(λ+cos θ))−1)g sin θ α=ω(dω/dθ)=((m_0 /m)×((λ+1)/(λ+cos θ))−1)(g/R) sin θ ∫_0 ^ω ωdω=∫_0 ^θ ((m_0 /m)×((λ+1)/(λ+cos θ))−1)(g/R) sin θdθ ⇒ω^2 =((2g)/R)∫_0 ^θ ((m_0 /m)×((λ+1)/(λ+cos θ))−1)sin θdθ mRω^2 =(F−mg) cos θ ⇒ω^2 =(g/R)((m_0 /m)×((λ+1)/(λ+cos θ))−1)cos θ ((m_0 /m)×((λ+1)/(λ+cos θ))−1)cos θ=2∫_0 ^θ ((m_0 /m)×((λ+1)/(λ+cos θ))−1) sin θdθ (((λ+1)/(λ+cos θ))−(m/m_0 ))cos θ=2∫_0 ^θ (((λ+1)/(λ+cos θ))−(m/m_0 )) sin θdθ since density of air is much smaller than that of water, (m/m_0 )=(ρ_(Air) /ρ_W )≈0. ((λ+1)/(λ+cos θ))cos θ=2∫_0 ^θ ((λ+1)/(λ+cos θ)) sin θdθ ((cos θ)/(λ+cos θ))=−2∫_0 ^θ ((d(λ+cos θ))/(λ+cos θ)) ⇒((cos θ)/(λ+cos θ))=2ln ((λ+1)/(λ+cos θ)) we get θ from it. (b/a)=(r/r_0 )=(((λ+1)/(λ+cos θ)))^(1/3) examples: λ=(h/R)=1: θ≈49.90°, (b/a)≈1.07 λ=(h/R)=5: θ≈48.69°, (b/a)≈1.53 λ=(h/R)=10: θ≈48.46°, (b/a)≈1.88
$${assume}: \\ $$$${air}\:{bubble}\:{is}\:{very}\:{small}\:{compared}\:{with}\: \\ $$$${the}\:{sphere}. \\ $$$${there}\:{is}\:{no}\:{resistance}\:{with}\:{water}. \\ $$$${there}\:{is}\:{no}\:{resistance}\:{with}\:{surface} \\ $$$${of}\:{sphere}. \\ $$$${r}_{\mathrm{0}} ={radius}\:{of}\:{bubble}\:{at}\:{O}. \\ $$$${r}={radius}\:{of}\:{bubble}\:{at}\:{T}. \\ $$$${m}={mass}\:{of}\:{air}\:{bubble}. \\ $$$$\rho_{{W}} ={density}\:{of}\:{water}. \\ $$$${h}={equivalent}\:{depth}\:{of}\:{center}\:{of}\:{sphere}. \\ $$$${let}\:\lambda=\frac{{h}}{{R}} \\ $$$$\frac{{V}}{{V}_{\mathrm{0}} }=\frac{{r}^{\mathrm{3}} }{{r}_{\mathrm{0}} ^{\mathrm{3}} }=\frac{{h}+{R}}{{h}+{R}\:\mathrm{cos}\:\theta}=\frac{\lambda+\mathrm{1}}{\lambda+\mathrm{cos}\:\theta} \\ $$$${F}=\frac{\mathrm{4}\pi\rho_{{W}} {gr}^{\mathrm{3}} }{\mathrm{3}} \\ $$$${F}=\frac{\mathrm{4}\pi\rho_{{W}} {gr}_{\mathrm{0}} ^{\mathrm{3}} }{\mathrm{3}}\left(\frac{\lambda+\mathrm{1}}{\lambda+\mathrm{cos}\:\theta}\right) \\ $$$${F}={m}_{\mathrm{0}} {g}\left(\frac{\lambda+\mathrm{1}}{\lambda+\mathrm{cos}\:\theta}\right)\:{with}\:{m}_{\mathrm{0}} =\frac{\mathrm{4}\pi\rho_{{W}} {r}_{\mathrm{0}} ^{\mathrm{3}} }{\mathrm{3}} \\ $$$${F}_{{R}} =\left({F}−{mg}\right)\:\mathrm{cos}\:\theta \\ $$$${F}_{\theta} =\left({F}−{mg}\right)\:\mathrm{sin}\:\theta \\ $$$$\omega=\frac{{d}\theta}{{dt}} \\ $$$$\alpha=\frac{{d}\omega}{{dt}}=\omega\frac{{d}\omega}{{d}\theta} \\ $$$${mR}\alpha=\left({F}−{mg}\right)\:\mathrm{sin}\:\theta \\ $$$${R}\alpha=\left(\frac{{m}_{\mathrm{0}} }{{m}}×\frac{\lambda+\mathrm{1}}{\lambda+\mathrm{cos}\:\theta}−\mathrm{1}\right){g}\:\mathrm{sin}\:\theta \\ $$$$\alpha=\omega\frac{{d}\omega}{{d}\theta}=\left(\frac{{m}_{\mathrm{0}} }{{m}}×\frac{\lambda+\mathrm{1}}{\lambda+\mathrm{cos}\:\theta}−\mathrm{1}\right)\frac{{g}}{{R}}\:\mathrm{sin}\:\theta \\ $$$$\int_{\mathrm{0}} ^{\omega} \omega{d}\omega=\int_{\mathrm{0}} ^{\theta} \left(\frac{{m}_{\mathrm{0}} }{{m}}×\frac{\lambda+\mathrm{1}}{\lambda+\mathrm{cos}\:\theta}−\mathrm{1}\right)\frac{{g}}{{R}}\:\mathrm{sin}\:\theta{d}\theta \\ $$$$\Rightarrow\omega^{\mathrm{2}} =\frac{\mathrm{2}{g}}{{R}}\int_{\mathrm{0}} ^{\theta} \left(\frac{{m}_{\mathrm{0}} }{{m}}×\frac{\lambda+\mathrm{1}}{\lambda+\mathrm{cos}\:\theta}−\mathrm{1}\right)\mathrm{sin}\:\theta{d}\theta \\ $$$${mR}\omega^{\mathrm{2}} =\left({F}−{mg}\right)\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow\omega^{\mathrm{2}} =\frac{{g}}{{R}}\left(\frac{{m}_{\mathrm{0}} }{{m}}×\frac{\lambda+\mathrm{1}}{\lambda+\mathrm{cos}\:\theta}−\mathrm{1}\right)\mathrm{cos}\:\theta \\ $$$$\left(\frac{{m}_{\mathrm{0}} }{{m}}×\frac{\lambda+\mathrm{1}}{\lambda+\mathrm{cos}\:\theta}−\mathrm{1}\right)\mathrm{cos}\:\theta=\mathrm{2}\int_{\mathrm{0}} ^{\theta} \left(\frac{{m}_{\mathrm{0}} }{{m}}×\frac{\lambda+\mathrm{1}}{\lambda+\mathrm{cos}\:\theta}−\mathrm{1}\right)\:\mathrm{sin}\:\theta{d}\theta \\ $$$$\left(\frac{\lambda+\mathrm{1}}{\lambda+\mathrm{cos}\:\theta}−\frac{{m}}{{m}_{\mathrm{0}} }\right)\mathrm{cos}\:\theta=\mathrm{2}\int_{\mathrm{0}} ^{\theta} \left(\frac{\lambda+\mathrm{1}}{\lambda+\mathrm{cos}\:\theta}−\frac{{m}}{{m}_{\mathrm{0}} }\right)\:\mathrm{sin}\:\theta{d}\theta \\ $$$${since}\:{density}\:{of}\:{air}\:{is}\:{much}\:{smaller} \\ $$$${than}\:{that}\:{of}\:{water},\:\frac{{m}}{{m}_{\mathrm{0}} }=\frac{\rho_{{Air}} }{\rho_{{W}} }\approx\mathrm{0}. \\ $$$$\frac{\lambda+\mathrm{1}}{\lambda+\mathrm{cos}\:\theta}\mathrm{cos}\:\theta=\mathrm{2}\int_{\mathrm{0}} ^{\theta} \frac{\lambda+\mathrm{1}}{\lambda+\mathrm{cos}\:\theta}\:\mathrm{sin}\:\theta{d}\theta \\ $$$$\frac{\mathrm{cos}\:\theta}{\lambda+\mathrm{cos}\:\theta}=−\mathrm{2}\int_{\mathrm{0}} ^{\theta} \frac{{d}\left(\lambda+\mathrm{cos}\:\theta\right)}{\lambda+\mathrm{cos}\:\theta} \\ $$$$\Rightarrow\frac{\mathrm{cos}\:\theta}{\lambda+\mathrm{cos}\:\theta}=\mathrm{2ln}\:\frac{\lambda+\mathrm{1}}{\lambda+\mathrm{cos}\:\theta} \\ $$$${we}\:{get}\:\theta\:{from}\:{it}. \\ $$$$\frac{{b}}{{a}}=\frac{{r}}{{r}_{\mathrm{0}} }=\sqrt[{\mathrm{3}}]{\frac{\lambda+\mathrm{1}}{\lambda+\mathrm{cos}\:\theta}} \\ $$$$ \\ $$$${examples}: \\ $$$$\lambda=\frac{{h}}{{R}}=\mathrm{1}:\:\theta\approx\mathrm{49}.\mathrm{90}°,\:\frac{{b}}{{a}}\approx\mathrm{1}.\mathrm{07} \\ $$$$\lambda=\frac{{h}}{{R}}=\mathrm{5}:\:\theta\approx\mathrm{48}.\mathrm{69}°,\:\frac{{b}}{{a}}\approx\mathrm{1}.\mathrm{53} \\ $$$$\lambda=\frac{{h}}{{R}}=\mathrm{10}:\:\theta\approx\mathrm{48}.\mathrm{46}°,\:\frac{{b}}{{a}}\approx\mathrm{1}.\mathrm{88} \\ $$
Commented by ajfour last updated on 22/Apr/21
Thanks sir, beautiful answer; I haven′t had enough leisure time..
$${Thanks}\:{sir},\:{beautiful}\:{answer}; \\ $$$${I}\:{haven}'{t}\:{had}\:{enough}\:{leisure}\:{time}.. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *