Question Number 139032 by bramlexs22 last updated on 21/Apr/21
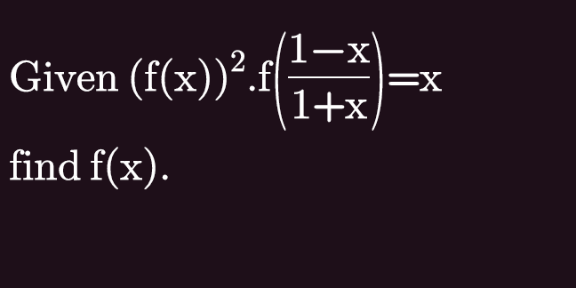
Answered by EDWIN88 last updated on 21/Apr/21
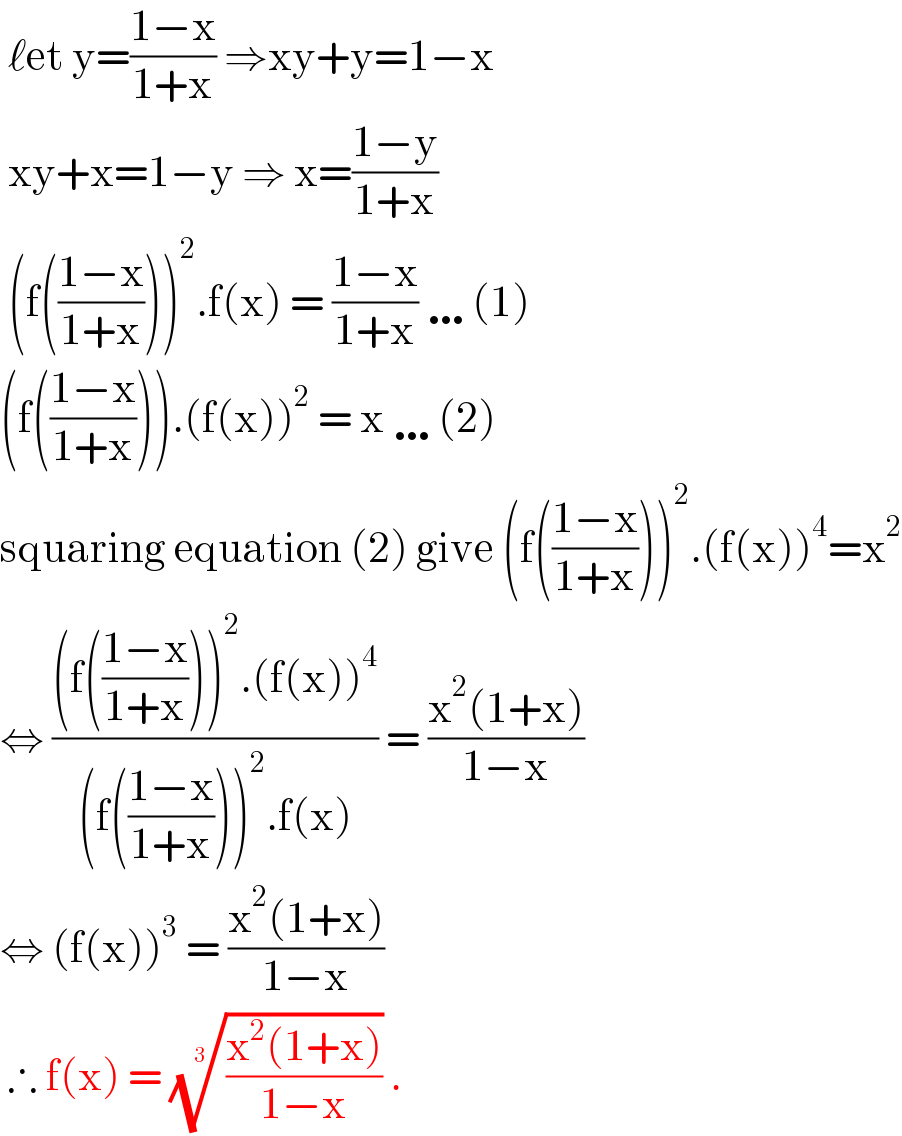
$$\:\ell\mathrm{et}\:\mathrm{y}=\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}\:\Rightarrow\mathrm{xy}+\mathrm{y}=\mathrm{1}−\mathrm{x}\: \\ $$$$\:\mathrm{xy}+\mathrm{x}=\mathrm{1}−\mathrm{y}\:\Rightarrow\:\mathrm{x}=\frac{\mathrm{1}−\mathrm{y}}{\mathrm{1}+\mathrm{x}} \\ $$$$\:\left(\mathrm{f}\left(\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}\right)\right)^{\mathrm{2}} .\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}\:\ldots\left(\mathrm{1}\right) \\ $$$$\left(\mathrm{f}\left(\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}\right)\right).\left(\mathrm{f}\left(\mathrm{x}\right)\right)^{\mathrm{2}} \:=\:\mathrm{x}\:\ldots\left(\mathrm{2}\right) \\ $$$$\mathrm{squaring}\:\mathrm{equation}\:\left(\mathrm{2}\right)\:\mathrm{give}\:\left(\mathrm{f}\left(\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}\right)\right)^{\mathrm{2}} .\left(\mathrm{f}\left(\mathrm{x}\right)\right)^{\mathrm{4}} =\mathrm{x}^{\mathrm{2}} \\ $$$$\Leftrightarrow\:\frac{\left(\mathrm{f}\left(\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}\right)\right)^{\mathrm{2}} .\left(\mathrm{f}\left(\mathrm{x}\right)\right)^{\mathrm{4}} }{\left(\mathrm{f}\left(\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}\right)\right)^{\mathrm{2}} .\mathrm{f}\left(\mathrm{x}\right)}\:=\:\frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}−\mathrm{x}} \\ $$$$\Leftrightarrow\:\left(\mathrm{f}\left(\mathrm{x}\right)\right)^{\mathrm{3}} \:=\:\frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}−\mathrm{x}}\: \\ $$$$\:\therefore\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}−\mathrm{x}}}\:.\: \\ $$
