Question Number 139053 by mathocean1 last updated on 21/Apr/21
Commented by mathocean1 last updated on 21/Apr/21

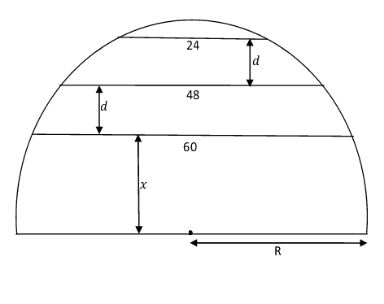
$${Determinate}\:{R} \\ $$
Answered by mr W last updated on 21/Apr/21
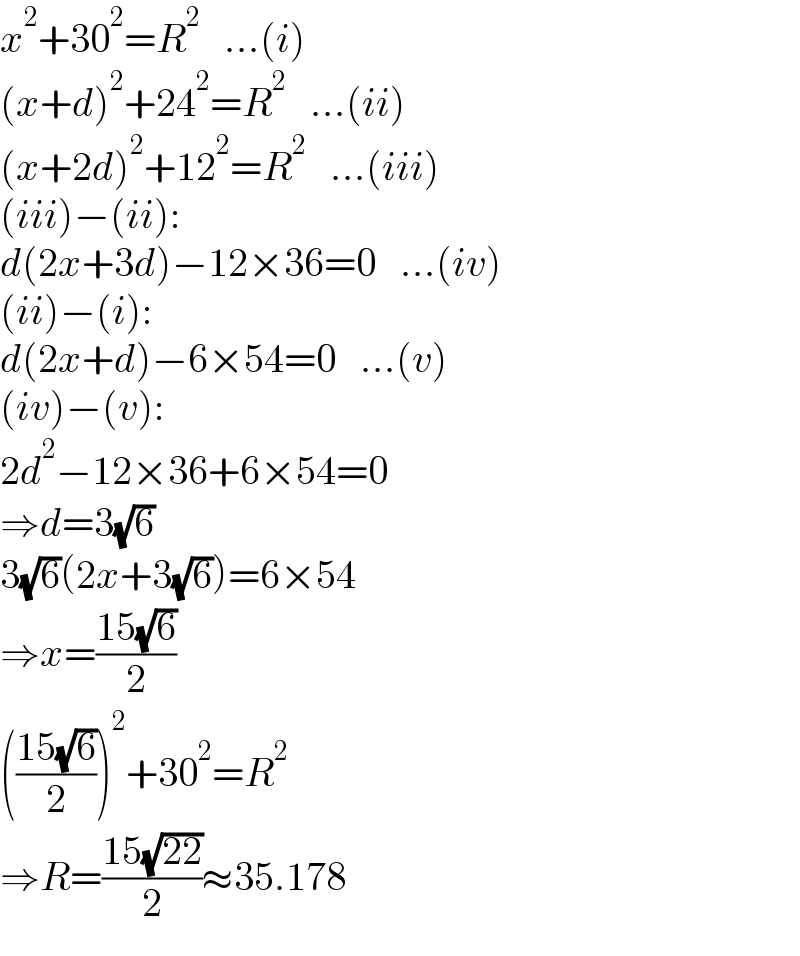
$${x}^{\mathrm{2}} +\mathrm{30}^{\mathrm{2}} ={R}^{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$$\left({x}+{d}\right)^{\mathrm{2}} +\mathrm{24}^{\mathrm{2}} ={R}^{\mathrm{2}} \:\:\:…\left({ii}\right) \\ $$$$\left({x}+\mathrm{2}{d}\right)^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} ={R}^{\mathrm{2}} \:\:\:…\left({iii}\right) \\ $$$$\left({iii}\right)−\left({ii}\right): \\ $$$${d}\left(\mathrm{2}{x}+\mathrm{3}{d}\right)−\mathrm{12}×\mathrm{36}=\mathrm{0}\:\:\:…\left({iv}\right) \\ $$$$\left({ii}\right)−\left({i}\right): \\ $$$${d}\left(\mathrm{2}{x}+{d}\right)−\mathrm{6}×\mathrm{54}=\mathrm{0}\:\:\:…\left({v}\right) \\ $$$$\left({iv}\right)−\left({v}\right): \\ $$$$\mathrm{2}{d}^{\mathrm{2}} −\mathrm{12}×\mathrm{36}+\mathrm{6}×\mathrm{54}=\mathrm{0} \\ $$$$\Rightarrow{d}=\mathrm{3}\sqrt{\mathrm{6}} \\ $$$$\mathrm{3}\sqrt{\mathrm{6}}\left(\mathrm{2}{x}+\mathrm{3}\sqrt{\mathrm{6}}\right)=\mathrm{6}×\mathrm{54} \\ $$$$\Rightarrow{x}=\frac{\mathrm{15}\sqrt{\mathrm{6}}}{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{15}\sqrt{\mathrm{6}}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{30}^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\Rightarrow{R}=\frac{\mathrm{15}\sqrt{\mathrm{22}}}{\mathrm{2}}\approx\mathrm{35}.\mathrm{178} \\ $$
