Question Number 139075 by bramlexs22 last updated on 22/Apr/21
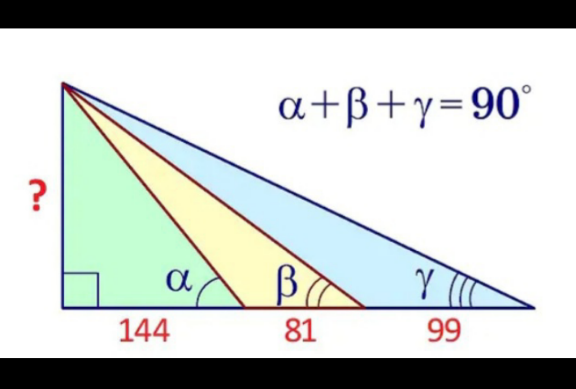
Answered by mr W last updated on 22/Apr/21

$$\mathrm{tan}\:\alpha=\frac{{x}}{\mathrm{144}} \\ $$$$\mathrm{tan}\:\beta=\frac{{x}}{\mathrm{144}+\mathrm{81}}=\frac{{x}}{\mathrm{225}} \\ $$$$\mathrm{tan}\:\gamma=\frac{{x}}{\mathrm{225}+\mathrm{99}}=\frac{{x}}{\mathrm{324}} \\ $$$$\mathrm{tan}\:\gamma=\mathrm{tan}\:\left(\mathrm{90}°−\alpha−\beta\right)=\frac{\mathrm{1}}{\mathrm{tan}\:\left(\alpha+\beta\right)} \\ $$$$\frac{{x}}{\mathrm{324}}=\frac{\mathrm{1}−\frac{{x}}{\mathrm{144}}×\frac{{x}}{\mathrm{225}}}{\frac{{x}}{\mathrm{144}}+\frac{{x}}{\mathrm{225}}}=\frac{\mathrm{3600}}{\mathrm{41}{x}}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{32400}}\right) \\ $$$$\mathrm{77}{x}^{\mathrm{2}} =\mathrm{36}×\mathrm{32400} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1080}}{\:\sqrt{\mathrm{77}}}\approx\mathrm{123}.\mathrm{077} \\ $$
