Question Number 139106 by mr W last updated on 23/Apr/21
Commented by mr W last updated on 25/Apr/21

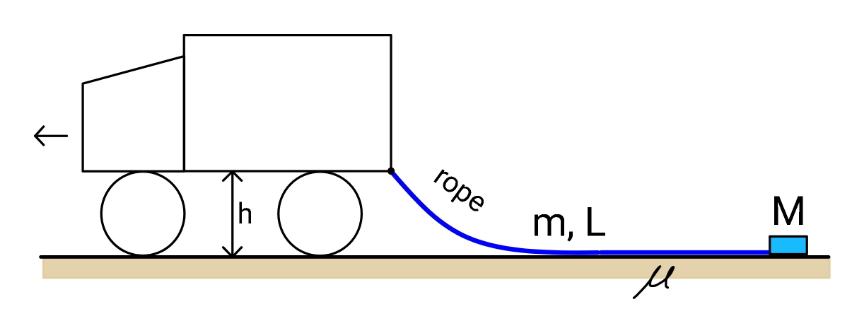
$${an}\:{uniform}\:{dense}\:{rope}\:{with}\:{length}\:\boldsymbol{{L}}\: \\ $$$${and}\:{mass}\:\boldsymbol{{m}}\:{is}\:{pulled}\:{by}\:{a}\:{truck}\:{with} \\ $$$${constant}\:{speed}.\:{on}\:{the}\:{end}\:{of}\:{rope}\:{a} \\ $$$${mass}\:\boldsymbol{{M}}\:{is}\:{connected}.\:{if}\:{the}\:{friction} \\ $$$${coefficient}\:{on}\:{the}\:{road}\:{surface}\:{is}\:\boldsymbol{\mu},\: \\ $$$${find}\:{the}\:{force}\:{the}\:{truck}\:{applies}\:{to} \\ $$$${the}\:{rope}. \\ $$
Answered by mr W last updated on 23/Apr/21
Commented by mr W last updated on 27/Apr/21
=0 (dk/dη)≠0 ⇒k=((μ^2 (1+ξ))/(1+μ^2 ))=(√((1+μ^2 )η^2 +2μη(1+ξ)))−μη ((μ^2 (1+ξ))/(1+μ^2 ))+μη=(√((1+μ^2 )η^2 +2μη(1+ξ))) ((μ^4 (1+ξ)^2 )/((1+μ^2 )^2 ))+μ^2 η^2 +((2μ^3 η(1+ξ))/(1+μ^2 ))=(1+μ^2 )η^2 +2μη(1+ξ) η^2 +((2μη(1+ξ))/(1+μ^2 ))−((μ^4 (1+ξ)^2 )/((1+μ^2 )^2 ))=0 ⇒η=((μ(1+ξ)((√(1+μ^2 ))−1))/(1+μ^2 ))](https://www.tinkutara.com/question/Q139158.png)
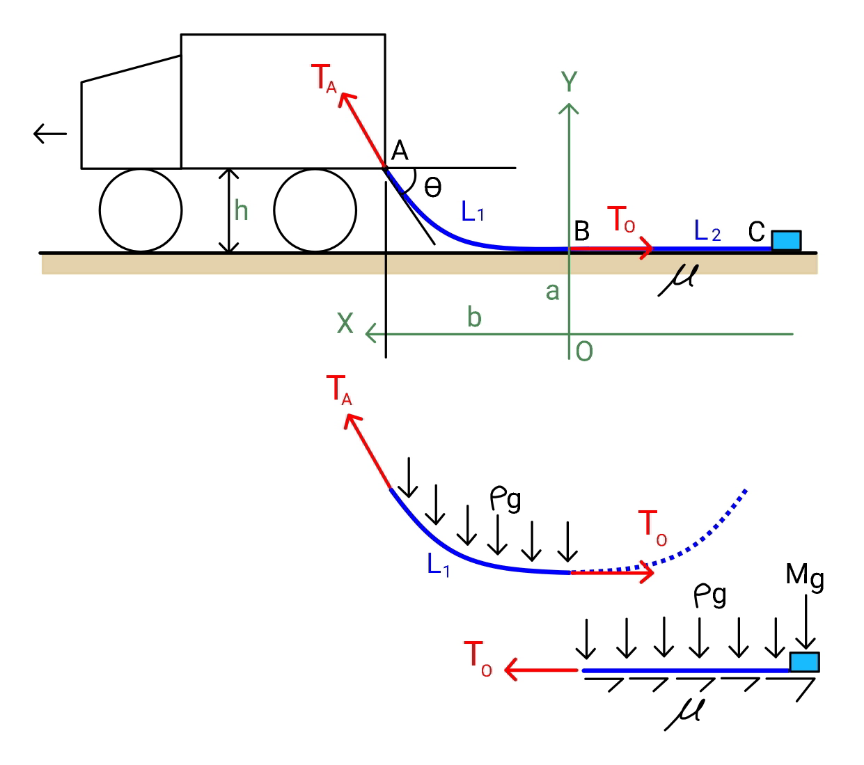
$${let}\:\rho=\frac{{m}}{{L}},\:\xi=\frac{{M}}{{m}},\:\eta=\frac{{h}}{{L}} \\ $$$${rope}\:{section}\:{AB}:\:{length}\:{L}_{\mathrm{1}} \\ $$$${rope}\:{section}\:{BC}:\:{length}\:{L}_{\mathrm{2}} \\ $$$$ \\ $$$${tension}\:{in}\:{rope}\:{at}\:{B}\:{is}\:{T}_{\mathrm{0}} \\ $$$${T}_{\mathrm{0}} =\mu\left(\rho{L}_{\mathrm{2}} +{M}\right){g}\:\:\left(={max}.\:{friction}\:{force}\right) \\ $$$$\:\:\:\:\:\:=\mu\left(\frac{{L}−{L}_{\mathrm{1}} }{{L}}{m}+{M}\right){g} \\ $$$$\:\:\:\:\:\:=\mu\left(\mathrm{1}+\xi−\frac{{L}_{\mathrm{1}} }{{L}}\right){mg} \\ $$$$\:\:\:\:\:\:=\mu\left(\mathrm{1}+\xi−{k}\right){mg}\:{with}\:{k}=\frac{{L}_{\mathrm{1}} }{{L}}\leqslant\mathrm{1} \\ $$$$ \\ $$$${AB}\:{is}\:{a}\:{part}\:{of}\:{a}\:{catenary}. \\ $$$${eqn}.\:{of}\:{catenary}\:{is} \\ $$$${y}={a}\:\mathrm{cosh}\:\frac{{x}}{{a}} \\ $$$${s}={a}\:\mathrm{sinh}\:\frac{{x}}{{a}}\:\left({length}\:{of}\:{rope}\:{upon}\:{B}\right) \\ $$$$\mathrm{tan}\:\theta={y}'=\mathrm{sinh}\:\frac{{x}}{{a}} \\ $$$${with}\:{a}=\frac{{T}_{\mathrm{0}} }{\rho{g}}=\frac{\mu\left(\mathrm{1}+\xi−{k}\right){mg}}{\rho{g}}=\mu{L}\left(\mathrm{1}+\xi−{k}\right) \\ $$$$ \\ $$$${at}\:{point}\:{A}: \\ $$$${y}={a}+{h}={a}\:\mathrm{cosh}\:\frac{{b}}{{a}} \\ $$$$\Rightarrow\mathrm{cosh}\:\frac{{b}}{{a}}=\frac{{a}+{h}}{{a}}\: \\ $$$${L}_{\mathrm{1}} ={a}\:\mathrm{sinh}\:\frac{{b}}{{a}} \\ $$$$\Rightarrow\mathrm{sinh}\:\frac{{b}}{{a}}=\frac{{L}_{\mathrm{1}} }{{a}}\: \\ $$$$\Rightarrow\frac{{b}}{{L}}=\mu\left(\mathrm{1}+\xi−{k}\right)\:\mathrm{sinh}^{−\mathrm{1}} \:\frac{{k}}{\mu\left(\mathrm{1}+\xi−{k}\right)} \\ $$$$\mathrm{tan}\:\theta=\mathrm{sinh}\:\frac{{b}}{{a}}=\frac{{L}_{\mathrm{1}} }{{a}}=\frac{{k}}{\mu\left(\mathrm{1}+\xi−{k}\right)} \\ $$$$ \\ $$$$\mathrm{cosh}^{\mathrm{2}} \:\frac{{b}}{{a}}−\mathrm{sinh}^{\mathrm{2}} \:\frac{{b}}{{a}}=\mathrm{1} \\ $$$$\Rightarrow\left(\frac{{a}+{h}}{{a}}\right)^{\mathrm{2}} −\left(\frac{{L}_{\mathrm{1}} }{{a}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +\mathrm{2}{ah}+{h}^{\mathrm{2}} −{L}_{\mathrm{1}} ^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}\mu{L}\left(\xi+\mathrm{1}−{k}\right){h}+{h}^{\mathrm{2}} −{L}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\mu\left(\xi+\mathrm{1}−{k}\right)\left(\frac{{h}}{{L}}\right)+\left(\frac{{h}}{{L}}\right)^{\mathrm{2}} −\left(\frac{{L}_{\mathrm{1}} }{{L}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{k}^{\mathrm{2}} +\mathrm{2}\mu\eta{k}−\mathrm{2}\mu\eta\left(\mathrm{1}+\xi\right)−\eta^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{k}=\sqrt{\left(\mathrm{1}+\mu^{\mathrm{2}} \right)\eta^{\mathrm{2}} +\mathrm{2}\mu\eta\left(\mathrm{1}+\xi\right)}−\mu\eta \\ $$$$ \\ $$$${force}\:{apllied}\:{by}\:{truck}\:{to}\:{rope}\:{is}\:{T}_{{A}} \\ $$$${T}_{{Ax}} ={T}_{\mathrm{0}} =\mu\left(\mathrm{1}+\xi−{k}\right){mg} \\ $$$${T}_{{Ay}} =\rho{gL}_{\mathrm{1}} ={kmg} \\ $$$$\Rightarrow{T}_{{A}} =\sqrt{{k}^{\mathrm{2}} +\mu^{\mathrm{2}} \left(\mathrm{1}+\xi−{k}\right)^{\mathrm{2}} }{mg} \\ $$$$ \\ $$$${such}\:{that}\:{k}\leqslant\mathrm{1}: \\ $$$$\sqrt{\left(\mathrm{1}+\mu^{\mathrm{2}} \right)\eta^{\mathrm{2}} +\mathrm{2}\mu\eta\left(\mathrm{1}+\xi\right)}−\mu\eta\leqslant\mathrm{1} \\ $$$$\left(\mathrm{1}+\mu^{\mathrm{2}} \right)\eta^{\mathrm{2}} +\mathrm{2}\mu\eta\left(\mathrm{1}+\xi\right)\leqslant\mathrm{1}+\mathrm{2}\mu\eta+\mu^{\mathrm{2}} \eta^{\mathrm{2}} \\ $$$$\eta^{\mathrm{2}} +\mathrm{2}\mu\xi\eta−\mathrm{1}\leqslant\mathrm{0} \\ $$$$\Rightarrow\eta\leqslant\sqrt{\mu^{\mathrm{2}} \xi^{\mathrm{2}} +\mathrm{1}}−\mu\xi \\ $$$$ \\ $$$$=================== \\ $$$$\Phi=\left(\frac{{T}_{{A}} }{{mg}}\right)^{\mathrm{2}} ={k}^{\mathrm{2}} +\mu^{\mathrm{2}} \left(\mathrm{1}+\xi−{k}\right)^{\mathrm{2}} \\ $$$${such}\:{that}\:{T}_{{A}} \:{is}\:{minimum}, \\ $$$$\frac{{d}\Phi}{{d}\eta}=\mathrm{2}{k}\frac{{dk}}{{d}\eta}−\mathrm{2}\mu^{\mathrm{2}} \left(\mathrm{1}+\xi−{k}\right)\frac{{dk}}{{d}\eta}=\mathrm{0} \\ $$$$\left[\left(\mathrm{1}+\mu^{\mathrm{2}} \right){k}−\mu^{\mathrm{2}} \left(\mathrm{1}+\xi\right)\right]\frac{{dk}}{{d}\eta}=\mathrm{0} \\ $$$$\frac{{dk}}{{d}\eta}\neq\mathrm{0} \\ $$$$\Rightarrow{k}=\frac{\mu^{\mathrm{2}} \left(\mathrm{1}+\xi\right)}{\mathrm{1}+\mu^{\mathrm{2}} }=\sqrt{\left(\mathrm{1}+\mu^{\mathrm{2}} \right)\eta^{\mathrm{2}} +\mathrm{2}\mu\eta\left(\mathrm{1}+\xi\right)}−\mu\eta \\ $$$$\frac{\mu^{\mathrm{2}} \left(\mathrm{1}+\xi\right)}{\mathrm{1}+\mu^{\mathrm{2}} }+\mu\eta=\sqrt{\left(\mathrm{1}+\mu^{\mathrm{2}} \right)\eta^{\mathrm{2}} +\mathrm{2}\mu\eta\left(\mathrm{1}+\xi\right)} \\ $$$$\frac{\mu^{\mathrm{4}} \left(\mathrm{1}+\xi\right)^{\mathrm{2}} }{\left(\mathrm{1}+\mu^{\mathrm{2}} \right)^{\mathrm{2}} }+\mu^{\mathrm{2}} \eta^{\mathrm{2}} +\frac{\mathrm{2}\mu^{\mathrm{3}} \eta\left(\mathrm{1}+\xi\right)}{\mathrm{1}+\mu^{\mathrm{2}} }=\left(\mathrm{1}+\mu^{\mathrm{2}} \right)\eta^{\mathrm{2}} +\mathrm{2}\mu\eta\left(\mathrm{1}+\xi\right) \\ $$$$\eta^{\mathrm{2}} +\frac{\mathrm{2}\mu\eta\left(\mathrm{1}+\xi\right)}{\mathrm{1}+\mu^{\mathrm{2}} }−\frac{\mu^{\mathrm{4}} \left(\mathrm{1}+\xi\right)^{\mathrm{2}} }{\left(\mathrm{1}+\mu^{\mathrm{2}} \right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\eta=\frac{\mu\left(\mathrm{1}+\xi\right)\left(\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }−\mathrm{1}\right)}{\mathrm{1}+\mu^{\mathrm{2}} } \\ $$
Commented by mr W last updated on 27/Apr/21
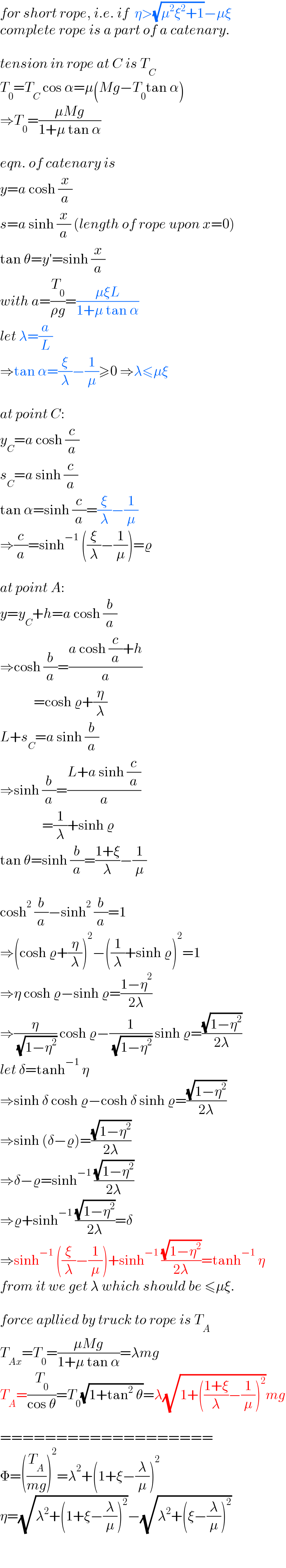
$${for}\:{short}\:{rope},\:{i}.{e}.\:{if}\:\:\eta>\sqrt{\mu^{\mathrm{2}} \xi^{\mathrm{2}} +\mathrm{1}}−\mu\xi \\ $$$${complete}\:{rope}\:{is}\:{a}\:{part}\:{of}\:{a}\:{catenary}. \\ $$$$ \\ $$$${tension}\:{in}\:{rope}\:{at}\:{C}\:{is}\:{T}_{{C}} \\ $$$${T}_{\mathrm{0}} ={T}_{{C}} \:\mathrm{cos}\:\alpha=\mu\left({Mg}−{T}_{\mathrm{0}} \mathrm{tan}\:\alpha\right) \\ $$$$\Rightarrow{T}_{\mathrm{0}} =\frac{\mu{Mg}}{\mathrm{1}+\mu\:\mathrm{tan}\:\alpha} \\ $$$$ \\ $$$${eqn}.\:{of}\:{catenary}\:{is} \\ $$$${y}={a}\:\mathrm{cosh}\:\frac{{x}}{{a}} \\ $$$${s}={a}\:\mathrm{sinh}\:\frac{{x}}{{a}}\:\left({length}\:{of}\:{rope}\:{upon}\:{x}=\mathrm{0}\right) \\ $$$$\mathrm{tan}\:\theta={y}'=\mathrm{sinh}\:\frac{{x}}{{a}} \\ $$$${with}\:{a}=\frac{{T}_{\mathrm{0}} }{\rho{g}}=\frac{\mu\xi{L}}{\mathrm{1}+\mu\:\mathrm{tan}\:\alpha} \\ $$$${let}\:\lambda=\frac{{a}}{{L}} \\ $$$$\Rightarrow\mathrm{tan}\:\alpha=\frac{\xi}{\lambda}−\frac{\mathrm{1}}{\mu}\geqslant\mathrm{0}\:\Rightarrow\lambda\leqslant\mu\xi \\ $$$$ \\ $$$${at}\:{point}\:{C}: \\ $$$${y}_{{C}} ={a}\:\mathrm{cosh}\:\frac{{c}}{{a}} \\ $$$${s}_{{C}} ={a}\:\mathrm{sinh}\:\frac{{c}}{{a}} \\ $$$$\mathrm{tan}\:\alpha=\mathrm{sinh}\:\frac{{c}}{{a}}=\frac{\xi}{\lambda}−\frac{\mathrm{1}}{\mu} \\ $$$$\Rightarrow\frac{{c}}{{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{\xi}{\lambda}−\frac{\mathrm{1}}{\mu}\right)=\varrho \\ $$$$ \\ $$$${at}\:{point}\:{A}: \\ $$$${y}={y}_{{C}} +{h}={a}\:\mathrm{cosh}\:\frac{{b}}{{a}} \\ $$$$\Rightarrow\mathrm{cosh}\:\frac{{b}}{{a}}=\frac{{a}\:\mathrm{cosh}\:\frac{{c}}{{a}}+{h}}{{a}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{cosh}\:\varrho+\frac{\eta}{\lambda} \\ $$$${L}+{s}_{{C}} ={a}\:\mathrm{sinh}\:\frac{{b}}{{a}} \\ $$$$\Rightarrow\mathrm{sinh}\:\frac{{b}}{{a}}=\frac{{L}+{a}\:\mathrm{sinh}\:\frac{{c}}{{a}}}{{a}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\lambda}+\mathrm{sinh}\:\varrho \\ $$$$\mathrm{tan}\:\theta=\mathrm{sinh}\:\frac{{b}}{{a}}=\frac{\mathrm{1}+\xi}{\lambda}−\frac{\mathrm{1}}{\mu} \\ $$$$ \\ $$$$\mathrm{cosh}^{\mathrm{2}} \:\frac{{b}}{{a}}−\mathrm{sinh}^{\mathrm{2}} \:\frac{{b}}{{a}}=\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{cosh}\:\varrho+\frac{\eta}{\lambda}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\lambda}+\mathrm{sinh}\:\varrho\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\eta\:\mathrm{cosh}\:\varrho−\mathrm{sinh}\:\varrho=\frac{\mathrm{1}−\eta^{\mathrm{2}} }{\mathrm{2}\lambda} \\ $$$$\Rightarrow\frac{\eta}{\:\sqrt{\mathrm{1}−\eta^{\mathrm{2}} }}\:\mathrm{cosh}\:\varrho−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\eta^{\mathrm{2}} }}\:\mathrm{sinh}\:\varrho=\frac{\sqrt{\mathrm{1}−\eta^{\mathrm{2}} }}{\mathrm{2}\lambda} \\ $$$${let}\:\delta=\mathrm{tanh}^{−\mathrm{1}} \:\eta \\ $$$$\Rightarrow\mathrm{sinh}\:\delta\:\mathrm{cosh}\:\varrho−\mathrm{cosh}\:\delta\:\mathrm{sinh}\:\varrho=\frac{\sqrt{\mathrm{1}−\eta^{\mathrm{2}} }}{\mathrm{2}\lambda} \\ $$$$\Rightarrow\mathrm{sinh}\:\left(\delta−\varrho\right)=\frac{\sqrt{\mathrm{1}−\eta^{\mathrm{2}} }}{\mathrm{2}\lambda} \\ $$$$\Rightarrow\delta−\varrho=\mathrm{sinh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{1}−\eta^{\mathrm{2}} }}{\mathrm{2}\lambda} \\ $$$$\Rightarrow\varrho+\mathrm{sinh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{1}−\eta^{\mathrm{2}} }}{\mathrm{2}\lambda}=\delta \\ $$$$\Rightarrow\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{\xi}{\lambda}−\frac{\mathrm{1}}{\mu}\right)+\mathrm{sinh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{1}−\eta^{\mathrm{2}} }}{\mathrm{2}\lambda}=\mathrm{tanh}^{−\mathrm{1}} \:\eta \\ $$$${from}\:{it}\:{we}\:{get}\:\lambda\:{which}\:{should}\:{be}\:\leqslant\mu\xi. \\ $$$$ \\ $$$${force}\:{apllied}\:{by}\:{truck}\:{to}\:{rope}\:{is}\:{T}_{{A}} \\ $$$${T}_{{Ax}} ={T}_{\mathrm{0}} =\frac{\mu{Mg}}{\mathrm{1}+\mu\:\mathrm{tan}\:\alpha}=\lambda{mg} \\ $$$${T}_{{A}} =\frac{{T}_{\mathrm{0}} }{\mathrm{cos}\:\theta}={T}_{\mathrm{0}} \sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta}=\lambda\sqrt{\mathrm{1}+\left(\frac{\mathrm{1}+\xi}{\lambda}−\frac{\mathrm{1}}{\mu}\right)^{\mathrm{2}} }{mg} \\ $$$$ \\ $$$$=================== \\ $$$$\Phi=\left(\frac{{T}_{{A}} }{{mg}}\right)^{\mathrm{2}} =\lambda^{\mathrm{2}} +\left(\mathrm{1}+\xi−\frac{\lambda}{\mu}\right)^{\mathrm{2}} \\ $$$$\eta=\sqrt{\lambda^{\mathrm{2}} +\left(\mathrm{1}+\xi−\frac{\lambda}{\mu}\right)^{\mathrm{2}} }−\sqrt{\lambda^{\mathrm{2}} +\left(\xi−\frac{\lambda}{\mu}\right)^{\mathrm{2}} } \\ $$
Commented by mr W last updated on 25/Apr/21
Commented by mr W last updated on 27/Apr/21
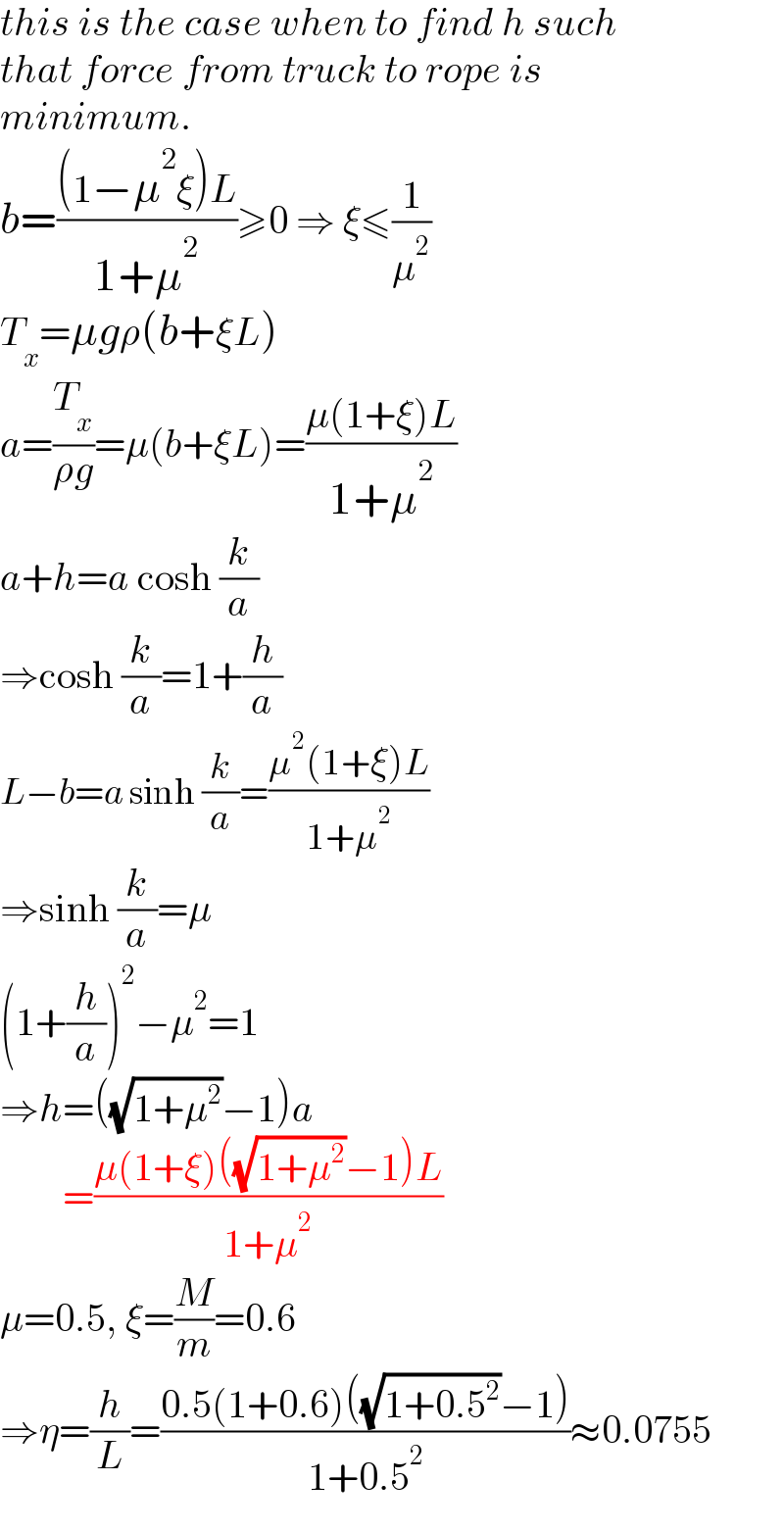
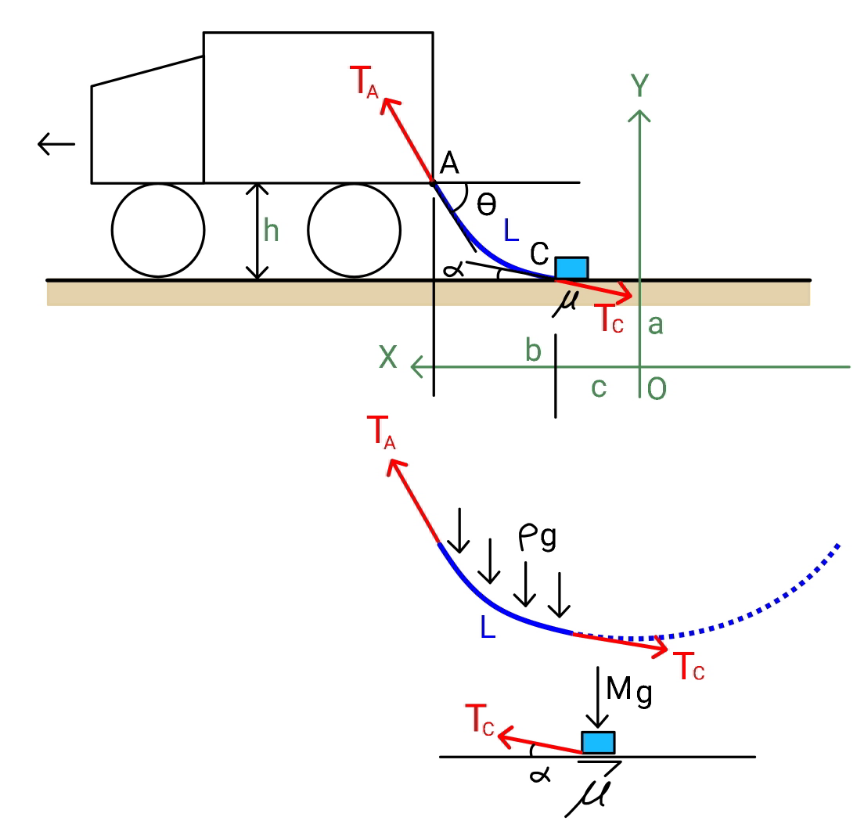
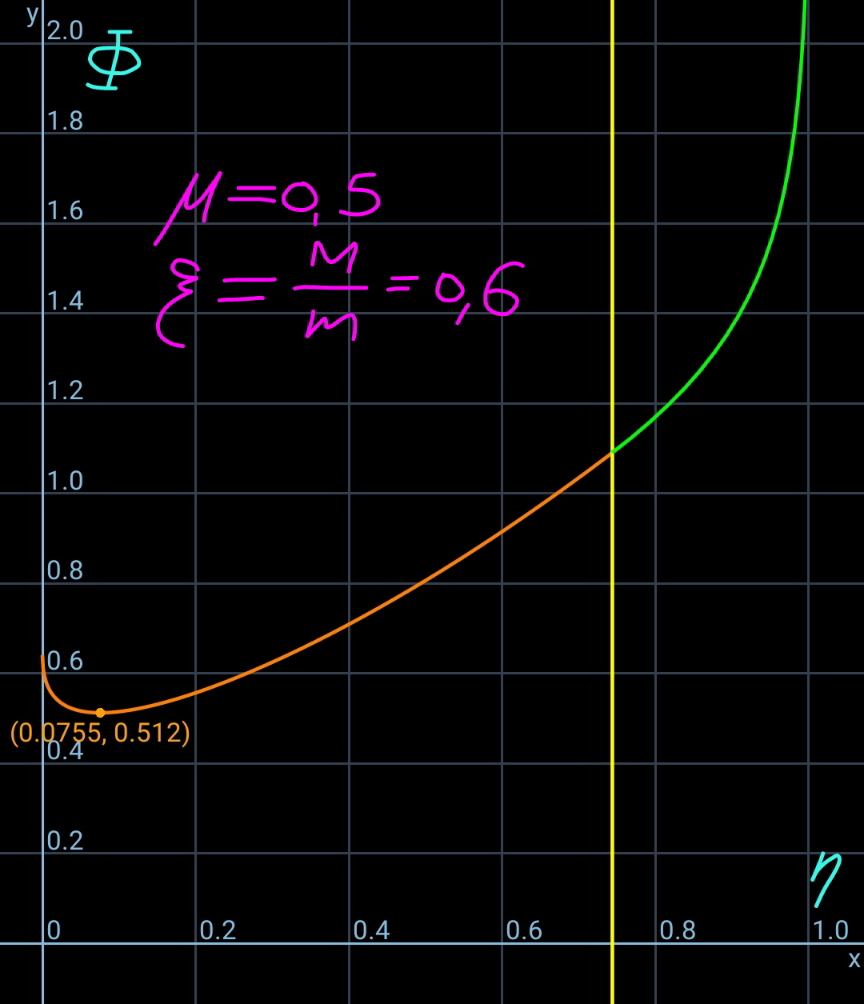
$${this}\:{is}\:{the}\:{case}\:{when}\:{to}\:{find}\:{h}\:{such} \\ $$$${that}\:{force}\:{from}\:{truck}\:{to}\:{rope}\:{is} \\ $$$${minimum}. \\ $$$${b}=\frac{\left(\mathrm{1}−\mu^{\mathrm{2}} \xi\right){L}}{\mathrm{1}+\mu^{\mathrm{2}} }\geqslant\mathrm{0}\:\Rightarrow\:\xi\leqslant\frac{\mathrm{1}}{\mu^{\mathrm{2}} } \\ $$$${T}_{{x}} =\mu{g}\rho\left({b}+\xi{L}\right) \\ $$$${a}=\frac{{T}_{{x}} }{\rho{g}}=\mu\left({b}+\xi{L}\right)=\frac{\mu\left(\mathrm{1}+\xi\right){L}}{\mathrm{1}+\mu^{\mathrm{2}} } \\ $$$${a}+{h}={a}\:\mathrm{cosh}\:\frac{{k}}{{a}} \\ $$$$\Rightarrow\mathrm{cosh}\:\frac{{k}}{{a}}=\mathrm{1}+\frac{{h}}{{a}} \\ $$$${L}−{b}={a}\:\mathrm{sinh}\:\frac{{k}}{{a}}=\frac{\mu^{\mathrm{2}} \left(\mathrm{1}+\xi\right){L}}{\mathrm{1}+\mu^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{sinh}\:\frac{{k}}{{a}}=\mu \\ $$$$\left(\mathrm{1}+\frac{{h}}{{a}}\right)^{\mathrm{2}} −\mu^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{h}=\left(\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }−\mathrm{1}\right){a} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mu\left(\mathrm{1}+\xi\right)\left(\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }−\mathrm{1}\right){L}}{\mathrm{1}+\mu^{\mathrm{2}} } \\ $$$$\mu=\mathrm{0}.\mathrm{5},\:\xi=\frac{{M}}{{m}}=\mathrm{0}.\mathrm{6} \\ $$$$\Rightarrow\eta=\frac{{h}}{{L}}=\frac{\mathrm{0}.\mathrm{5}\left(\mathrm{1}+\mathrm{0}.\mathrm{6}\right)\left(\sqrt{\mathrm{1}+\mathrm{0}.\mathrm{5}^{\mathrm{2}} }−\mathrm{1}\right)}{\mathrm{1}+\mathrm{0}.\mathrm{5}^{\mathrm{2}} }\approx\mathrm{0}.\mathrm{0755} \\ $$
Commented by ajfour last updated on 26/Apr/21
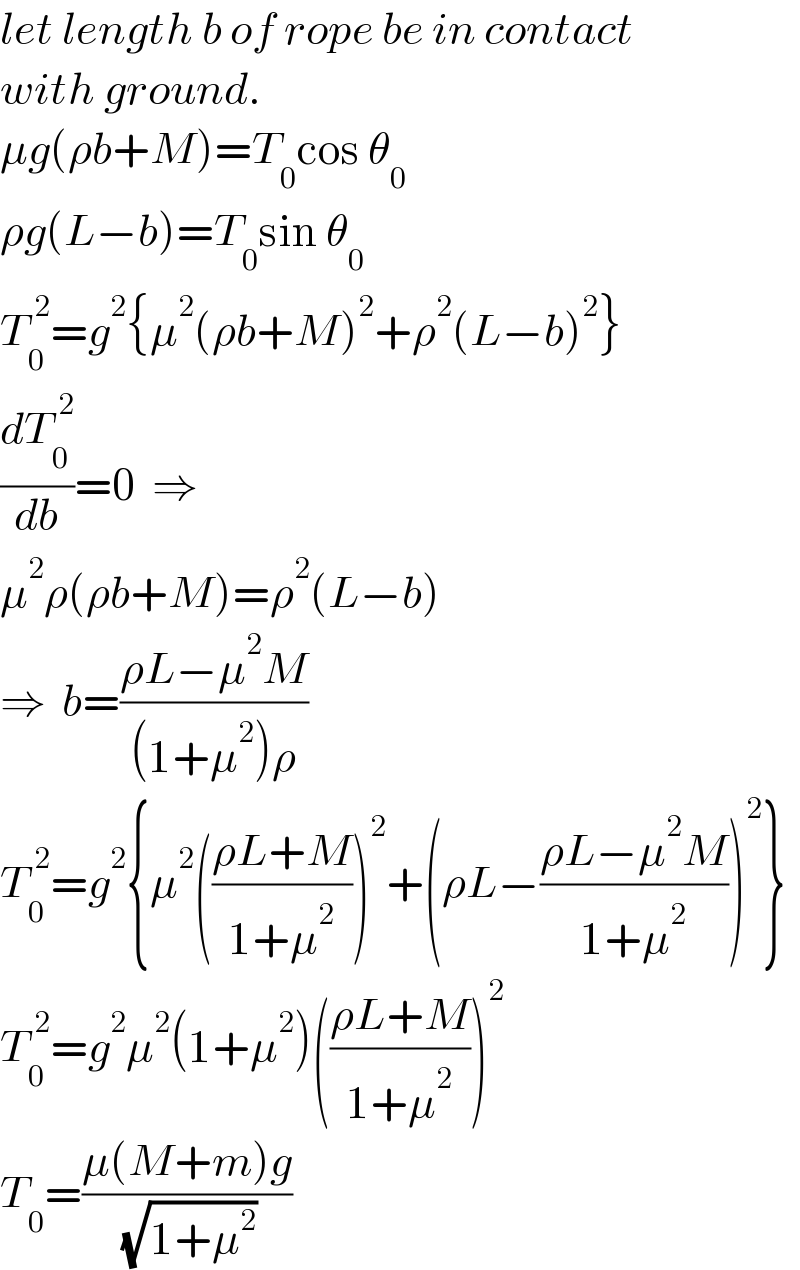
$${let}\:{length}\:{b}\:{of}\:{rope}\:{be}\:{in}\:{contact} \\ $$$${with}\:{ground}. \\ $$$$\mu{g}\left(\rho{b}+{M}\right)={T}_{\mathrm{0}} \mathrm{cos}\:\theta_{\mathrm{0}} \\ $$$$\rho{g}\left({L}−{b}\right)={T}_{\mathrm{0}} \mathrm{sin}\:\theta_{\mathrm{0}} \\ $$$${T}_{\mathrm{0}} ^{\:\mathrm{2}} ={g}^{\mathrm{2}} \left\{\mu^{\mathrm{2}} \left(\rho{b}+{M}\right)^{\mathrm{2}} +\rho^{\mathrm{2}} \left({L}−{b}\right)^{\mathrm{2}} \right\} \\ $$$$\frac{{dT}_{\mathrm{0}} ^{\:\mathrm{2}} }{{db}}=\mathrm{0}\:\:\Rightarrow \\ $$$$\mu^{\mathrm{2}} \rho\left(\rho{b}+{M}\right)=\rho^{\mathrm{2}} \left({L}−{b}\right) \\ $$$$\Rightarrow\:\:{b}=\frac{\rho{L}−\mu^{\mathrm{2}} {M}}{\left(\mathrm{1}+\mu^{\mathrm{2}} \right)\rho} \\ $$$${T}_{\mathrm{0}} ^{\:\mathrm{2}} ={g}^{\mathrm{2}} \left\{\mu^{\mathrm{2}} \left(\frac{\rho{L}+{M}}{\mathrm{1}+\mu^{\mathrm{2}} }\right)^{\mathrm{2}} +\left(\rho{L}−\frac{\rho{L}−\mu^{\mathrm{2}} {M}}{\mathrm{1}+\mu^{\mathrm{2}} }\right)^{\mathrm{2}} \right\} \\ $$$${T}_{\mathrm{0}} ^{\:\mathrm{2}} ={g}^{\mathrm{2}} \mu^{\mathrm{2}} \left(\mathrm{1}+\mu^{\mathrm{2}} \right)\left(\frac{\rho{L}+{M}}{\mathrm{1}+\mu^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$${T}_{\mathrm{0}} =\frac{\mu\left({M}+{m}\right){g}}{\:\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }} \\ $$
Commented by ajfour last updated on 26/Apr/21
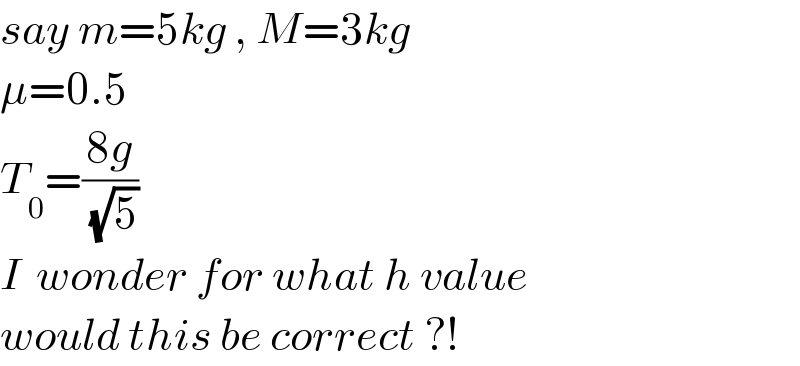
$${say}\:{m}=\mathrm{5}{kg}\:,\:{M}=\mathrm{3}{kg} \\ $$$$\mu=\mathrm{0}.\mathrm{5} \\ $$$${T}_{\mathrm{0}} =\frac{\mathrm{8}{g}}{\:\sqrt{\mathrm{5}}} \\ $$$${I}\:\:{wonder}\:{for}\:{what}\:{h}\:{value} \\ $$$${would}\:{this}\:{be}\:{correct}\:?! \\ $$
Commented by mr W last updated on 27/Apr/21

$${the}\:{same}\:{result}\:{can}\:{be}\:{obtained} \\ $$$${through}\:\frac{{dT}_{{A}} }{{d}\eta}=\mathrm{0}.\:{i}\:{have}\:{added}\:{this}\:{in} \\ $$$${my}\:{solution}. \\ $$
Commented by mr W last updated on 27/Apr/21
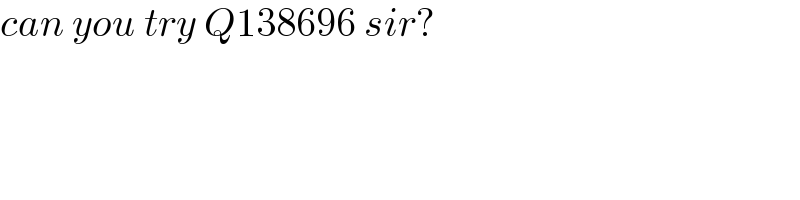
$${can}\:{you}\:{try}\:{Q}\mathrm{138696}\:{sir}? \\ $$
Commented by mr W last updated on 27/Apr/21
Commented by mr W last updated on 27/Apr/21
Commented by ajfour last updated on 27/Apr/21

$${yes}\:{sir}\:{i}\:{attemted}\:{once}\:{then}, \\ $$$${but}\:{forgot}\:{to}\:{pursue}\:{it}\:{sincerely}.. \\ $$
Commented by mr W last updated on 27/Apr/21
$${thanks}\:{sir}!\:{i}'{ll}\:{also}\:{make}\:{a}\:{try}. \\ $$
