Question Number 139165 by mathlove last updated on 23/Apr/21

Answered by mr W last updated on 23/Apr/21
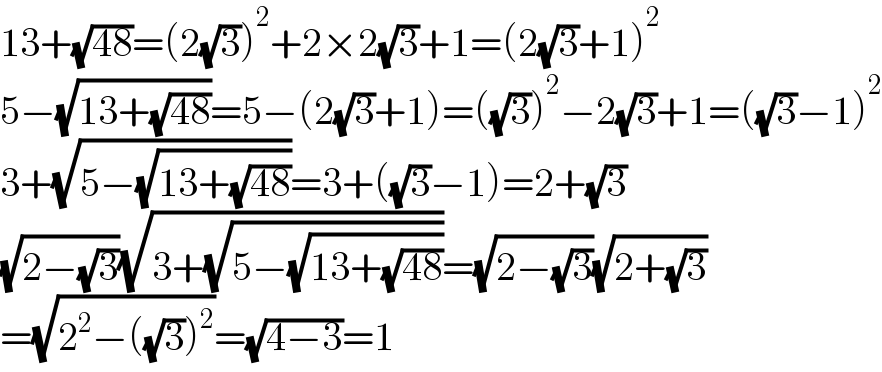
$$\mathrm{13}+\sqrt{\mathrm{48}}=\left(\mathrm{2}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{2}×\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{1}=\left(\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{5}−\sqrt{\mathrm{13}+\sqrt{\mathrm{48}}}=\mathrm{5}−\left(\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{1}\right)=\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{1}=\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{3}+\sqrt{\mathrm{5}−\sqrt{\mathrm{13}+\sqrt{\mathrm{48}}}}=\mathrm{3}+\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\sqrt{\mathrm{3}+\sqrt{\mathrm{5}−\sqrt{\mathrm{13}+\sqrt{\mathrm{48}}}}}=\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$$=\sqrt{\mathrm{2}^{\mathrm{2}} −\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }=\sqrt{\mathrm{4}−\mathrm{3}}=\mathrm{1} \\ $$
Commented by mathlove last updated on 23/Apr/21

$${thanks}\:\:\:{sir} \\ $$
Commented by greg_ed last updated on 23/Apr/21

$$\mathrm{cool}\:!\: \\ $$
