Question Number 139276 by mnjuly1970 last updated on 25/Apr/21

Commented by mnjuly1970 last updated on 28/Apr/21
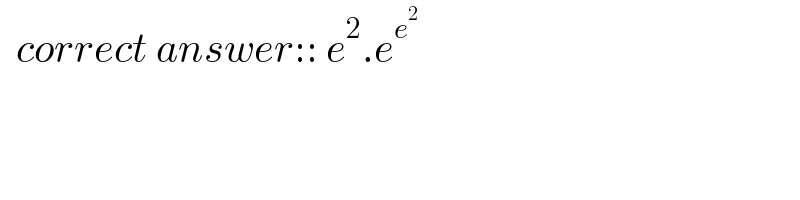
$$\:\:{correct}\:{answer}::\:{e}^{\mathrm{2}} .{e}^{{e}^{\mathrm{2}} } \\ $$
Answered by Dwaipayan Shikari last updated on 25/Apr/21
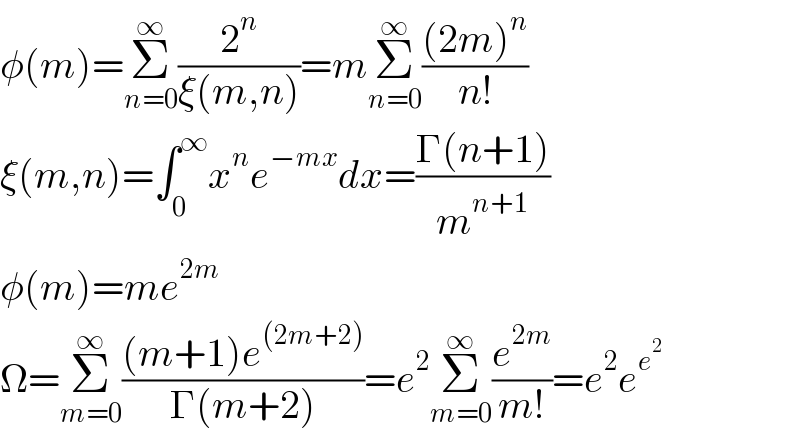
$$\phi\left({m}\right)=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{n}} }{\xi\left({m},{n}\right)}={m}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{2}{m}\right)^{{n}} }{{n}!} \\ $$$$\xi\left({m},{n}\right)=\int_{\mathrm{0}} ^{\infty} {x}^{{n}} {e}^{−{mx}} {dx}=\frac{\Gamma\left({n}+\mathrm{1}\right)}{{m}^{{n}+\mathrm{1}} } \\ $$$$\phi\left({m}\right)={me}^{\mathrm{2}{m}} \\ $$$$\Omega=\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({m}+\mathrm{1}\right){e}^{\left(\mathrm{2}{m}+\mathrm{2}\right)} }{\Gamma\left({m}+\mathrm{2}\right)}={e}^{\mathrm{2}} \underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{e}^{\mathrm{2}{m}} }{{m}!}={e}^{\mathrm{2}} {e}^{{e}^{\mathrm{2}} } \\ $$
