Question Number 139426 by I want to learn more last updated on 26/Apr/21

Answered by physicstutes last updated on 26/Apr/21
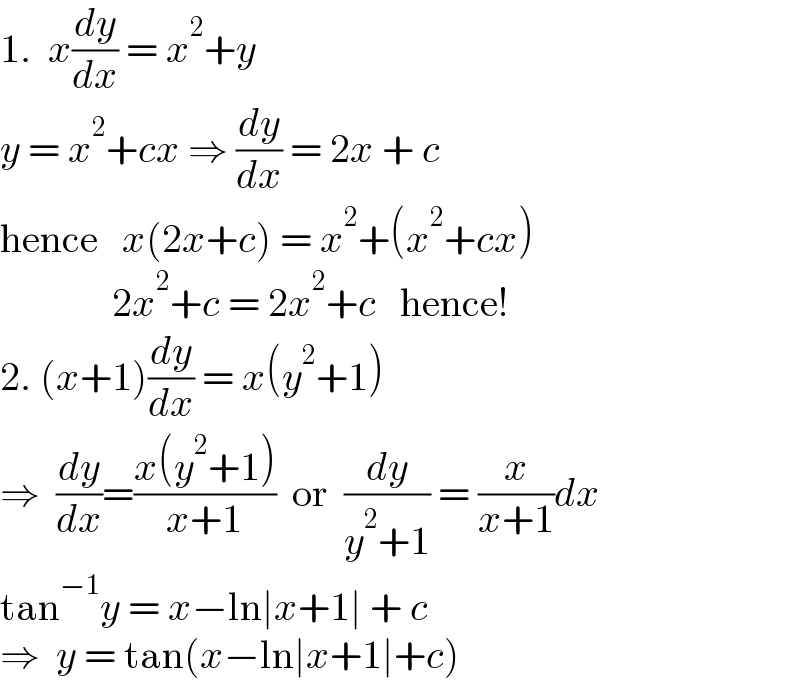
$$\mathrm{1}.\:\:{x}\frac{{dy}}{{dx}}\:=\:{x}^{\mathrm{2}} +{y} \\ $$$${y}\:=\:{x}^{\mathrm{2}} +{cx}\:\Rightarrow\:\frac{{dy}}{{dx}}\:=\:\mathrm{2}{x}\:+\:{c} \\ $$$$\mathrm{hence}\:\:\:{x}\left(\mathrm{2}{x}+{c}\right)\:=\:{x}^{\mathrm{2}} +\left({x}^{\mathrm{2}} +{cx}\right)\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{x}^{\mathrm{2}} +{c}\:=\:\mathrm{2}{x}^{\mathrm{2}} +{c}\:\:\:\mathrm{hence}! \\ $$$$\mathrm{2}.\:\left({x}+\mathrm{1}\right)\frac{{dy}}{{dx}}\:=\:{x}\left({y}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\Rightarrow\:\:\frac{{dy}}{{dx}}=\frac{{x}\left({y}^{\mathrm{2}} +\mathrm{1}\right)}{{x}+\mathrm{1}}\:\:\mathrm{or}\:\:\frac{{dy}}{{y}^{\mathrm{2}} +\mathrm{1}}\:=\:\frac{{x}}{{x}+\mathrm{1}}{dx} \\ $$$$\mathrm{tan}^{−\mathrm{1}} {y}\:=\:{x}−\mathrm{ln}\mid{x}+\mathrm{1}\mid\:+\:{c} \\ $$$$\Rightarrow\:\:{y}\:=\:\mathrm{tan}\left({x}−\mathrm{ln}\mid{x}+\mathrm{1}\mid+{c}\right) \\ $$
Commented by I want to learn more last updated on 28/Apr/21

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$
