Question Number 139454 by aliibrahim1 last updated on 27/Apr/21
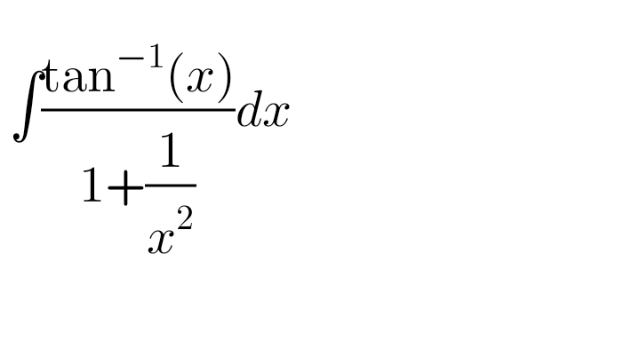
Answered by Dwaipayan Shikari last updated on 27/Apr/21
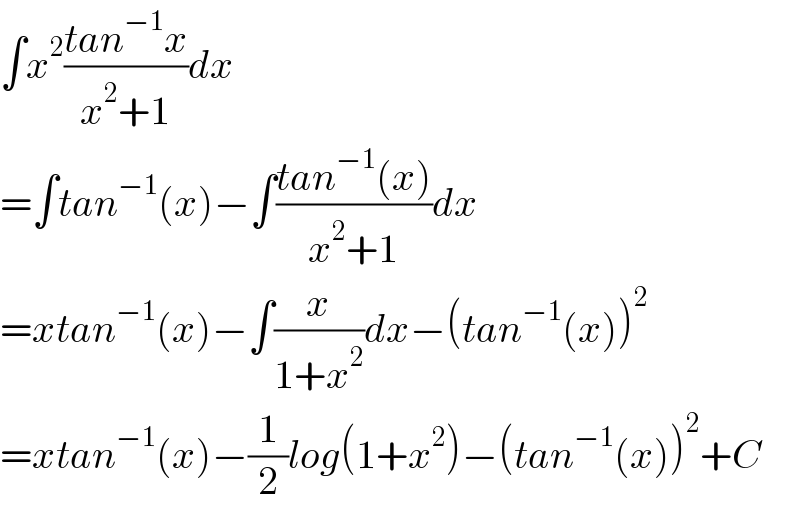
$$\int{x}^{\mathrm{2}} \frac{{tan}^{−\mathrm{1}} {x}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$=\int{tan}^{−\mathrm{1}} \left({x}\right)−\int\frac{{tan}^{−\mathrm{1}} \left({x}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$={xtan}^{−\mathrm{1}} \left({x}\right)−\int\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}−\left({tan}^{−\mathrm{1}} \left({x}\right)\right)^{\mathrm{2}} \\ $$$$={xtan}^{−\mathrm{1}} \left({x}\right)−\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\left({tan}^{−\mathrm{1}} \left({x}\right)\right)^{\mathrm{2}} +{C} \\ $$
Commented by aliibrahim1 last updated on 27/Apr/21

$${thx}\:{man} \\ $$
