Question Number 139476 by aliibrahim1 last updated on 27/Apr/21

Answered by qaz last updated on 27/Apr/21
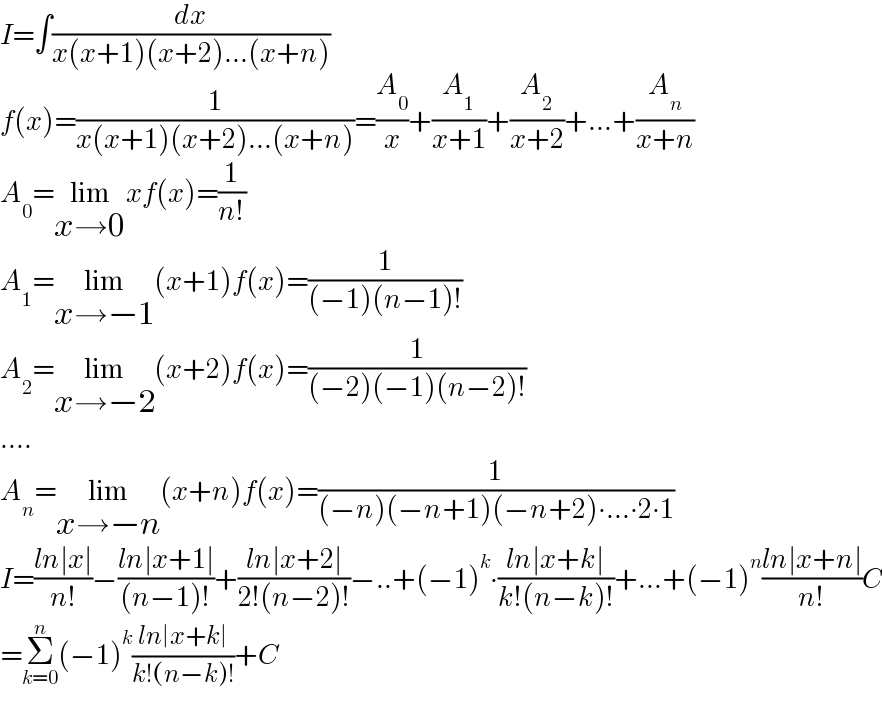
$${I}=\int\frac{{dx}}{{x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)…\left({x}+{n}\right)} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{{x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)…\left({x}+{n}\right)}=\frac{{A}_{\mathrm{0}} }{{x}}+\frac{{A}_{\mathrm{1}} }{{x}+\mathrm{1}}+\frac{{A}_{\mathrm{2}} }{{x}+\mathrm{2}}+…+\frac{{A}_{{n}} }{{x}+{n}} \\ $$$${A}_{\mathrm{0}} =\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{xf}\left({x}\right)=\frac{\mathrm{1}}{{n}!} \\ $$$${A}_{\mathrm{1}} =\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\left({x}+\mathrm{1}\right){f}\left({x}\right)=\frac{\mathrm{1}}{\left(−\mathrm{1}\right)\left({n}−\mathrm{1}\right)!} \\ $$$${A}_{\mathrm{2}} =\underset{{x}\rightarrow−\mathrm{2}} {\mathrm{lim}}\left({x}+\mathrm{2}\right){f}\left({x}\right)=\frac{\mathrm{1}}{\left(−\mathrm{2}\right)\left(−\mathrm{1}\right)\left({n}−\mathrm{2}\right)!} \\ $$$$…. \\ $$$${A}_{{n}} =\underset{{x}\rightarrow−{n}} {\mathrm{lim}}\left({x}+{n}\right){f}\left({x}\right)=\frac{\mathrm{1}}{\left(−{n}\right)\left(−{n}+\mathrm{1}\right)\left(−{n}+\mathrm{2}\right)\centerdot…\centerdot\mathrm{2}\centerdot\mathrm{1}} \\ $$$${I}=\frac{{ln}\mid{x}\mid}{{n}!}−\frac{{ln}\mid{x}+\mathrm{1}\mid}{\left({n}−\mathrm{1}\right)!}+\frac{{ln}\mid{x}+\mathrm{2}\mid}{\mathrm{2}!\left({n}−\mathrm{2}\right)!}−..+\left(−\mathrm{1}\right)^{{k}} \centerdot\frac{{ln}\mid{x}+{k}\mid}{{k}!\left({n}−{k}\right)!}+…+\left(−\mathrm{1}\right)^{{n}} \frac{{ln}\mid{x}+{n}\mid}{{n}!}{C} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \frac{{ln}\mid{x}+{k}\mid}{{k}!\left({n}−{k}\right)!}+{C} \\ $$
Commented by aliibrahim1 last updated on 27/Apr/21

$${thx}\:{sir} \\ $$
