Question-139599

Question Number 139599 by I want to learn more last updated on 29/Apr/21

Answered by mr W last updated on 29/Apr/21

Commented by mr W last updated on 29/Apr/21

“all forces” means including weight of block: F_4 =mg=10 N. x component of all forces: F_x =20×(4/5)+10×(3/5)+10×(4/5)+10×0=30N (→) y component of all forces: F_y =20×(3/5)+10×(4/5)−10×(3/5)−10×1=4N(↑) F=(√(30^2 +4^2 ))=2(√(229)) N ma=F a=(F/m) s=(1/2)at^2 =((Ft^2 )/(2m)) work done by all forces on the block: W=Fs=((F^2 t^2 )/(2m))=((4×229×1^2 )/(2×1))=458 J or W=E=(1/2)mv^2 =(1/2)m(at)^2 =((F^2 t^2 )/(2m))

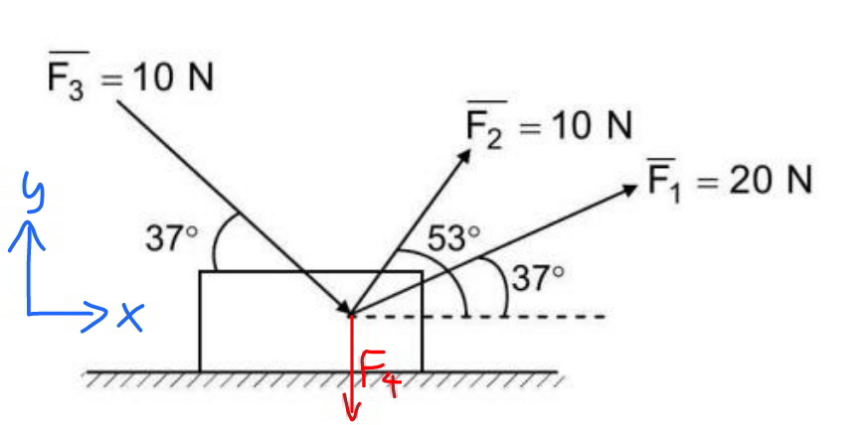
$$“{all}\:{forces}''\:{means}\:{including}\:{weight} \\ $$$${of}\:{block}:\:{F}_{\mathrm{4}} ={mg}=\mathrm{10}\:{N}. \\ $$$${x}\:{component}\:{of}\:{all}\:{forces}: \\ $$$${F}_{{x}} =\mathrm{20}×\frac{\mathrm{4}}{\mathrm{5}}+\mathrm{10}×\frac{\mathrm{3}}{\mathrm{5}}+\mathrm{10}×\frac{\mathrm{4}}{\mathrm{5}}+\mathrm{10}×\mathrm{0}=\mathrm{30}{N}\:\left(\rightarrow\right) \\ $$$${y}\:{component}\:{of}\:{all}\:{forces}: \\ $$$${F}_{{y}} =\mathrm{20}×\frac{\mathrm{3}}{\mathrm{5}}+\mathrm{10}×\frac{\mathrm{4}}{\mathrm{5}}−\mathrm{10}×\frac{\mathrm{3}}{\mathrm{5}}−\mathrm{10}×\mathrm{1}=\mathrm{4}{N}\left(\uparrow\right) \\ $$$${F}=\sqrt{\mathrm{30}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} }=\mathrm{2}\sqrt{\mathrm{229}}\:{N} \\ $$$${ma}={F} \\ $$$${a}=\frac{{F}}{{m}} \\ $$$${s}=\frac{\mathrm{1}}{\mathrm{2}}{at}^{\mathrm{2}} =\frac{{Ft}^{\mathrm{2}} }{\mathrm{2}{m}} \\ $$$${work}\:{done}\:{by}\:{all}\:{forces}\:{on}\:{the}\:{block}: \\ $$$${W}={Fs}=\frac{{F}^{\mathrm{2}} {t}^{\mathrm{2}} }{\mathrm{2}{m}}=\frac{\mathrm{4}×\mathrm{229}×\mathrm{1}^{\mathrm{2}} }{\mathrm{2}×\mathrm{1}}=\mathrm{458}\:{J} \\ $$$${or} \\ $$$${W}={E}=\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}{m}\left({at}\right)^{\mathrm{2}} =\frac{{F}^{\mathrm{2}} {t}^{\mathrm{2}} }{\mathrm{2}{m}} \\ $$

Commented by I want to learn more last updated on 29/Apr/21

Thanks sir. I really appreciate. God bless you sir.

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by Dwaipayan Shikari last updated on 29/Apr/21

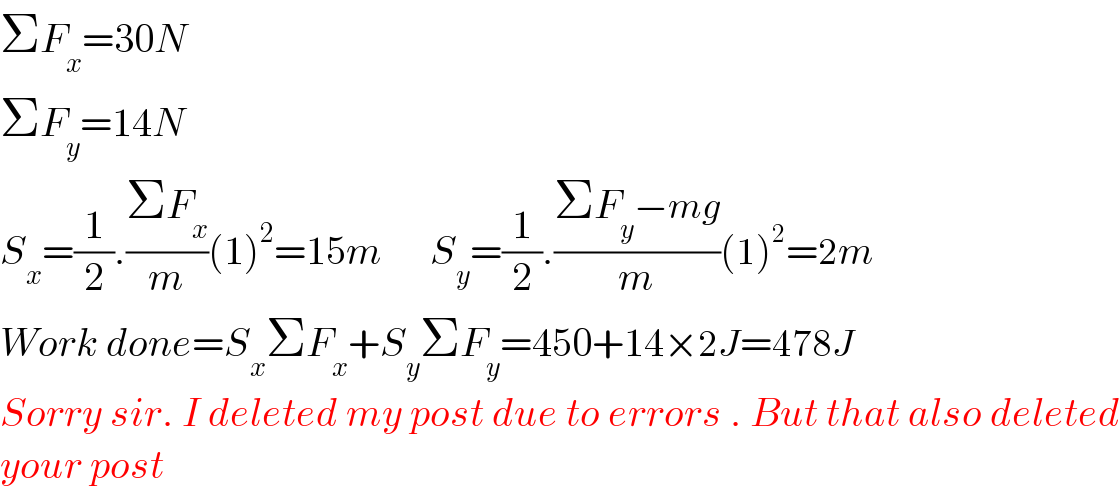
ΣF_x =30N ΣF_y =14N S_x =(1/2).((ΣF_x )/m)(1)^2 =15m S_y =(1/2).((ΣF_y −mg)/m)(1)^2 =2m Work done=S_x ΣF_x +S_y ΣF_y =450+14×2J=478J Sorry sir. I deleted my post due to errors . But that also deleted your post

$$\Sigma{F}_{{x}} =\mathrm{30}{N} \\ $$$$\Sigma{F}_{{y}} =\mathrm{14}{N} \\ $$$${S}_{{x}} =\frac{\mathrm{1}}{\mathrm{2}}.\frac{\Sigma{F}_{{x}} }{{m}}\left(\mathrm{1}\right)^{\mathrm{2}} =\mathrm{15}{m}\:\:\:\:\:\:{S}_{{y}} =\frac{\mathrm{1}}{\mathrm{2}}.\frac{\Sigma{F}_{{y}} −{mg}}{{m}}\left(\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2}{m} \\ $$$${Work}\:{done}={S}_{{x}} \Sigma{F}_{{x}} +{S}_{{y}} \Sigma{F}_{{y}} =\mathrm{450}+\mathrm{14}×\mathrm{2}{J}=\mathrm{478}{J} \\ $$$${Sorry}\:{sir}.\:{I}\:{deleted}\:{my}\:{post}\:{due}\:{to}\:{errors}\:.\:{But}\:{that}\:{also}\:{deleted} \\ $$$${your}\:{post}\: \\ $$

Commented by I want to learn more last updated on 29/Apr/21

Thanks sir. God bless you. I really appreciate.

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}.\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$

Commented by mr W last updated on 29/Apr/21

$${you}\:{are}\:{right}\:{sir}.\:{just}\:{one}\:{thing}: \\ $$$${the}\:{question}\:{says}\:{work}\:{done}\:{by}\:{all} \\ $$$${forces}\:{acting}\:{on}\:{the}\:{block}.\:\:{it}\:{should} \\ $$$${also}\:{include}\:{the}\:{gravity}\:{force},\:{which} \\ $$$${did}\:{a}\:{work}\:{in}\:{y}\:{direction}:\:−\mathrm{10}×\mathrm{2}=−\mathrm{20}\:{J}. \\ $$

Commented by Tawa11 last updated on 14/Sep/21

$$\mathrm{nice} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply