Question Number 139600 by rexford last updated on 29/Apr/21

Answered by mr W last updated on 29/Apr/21
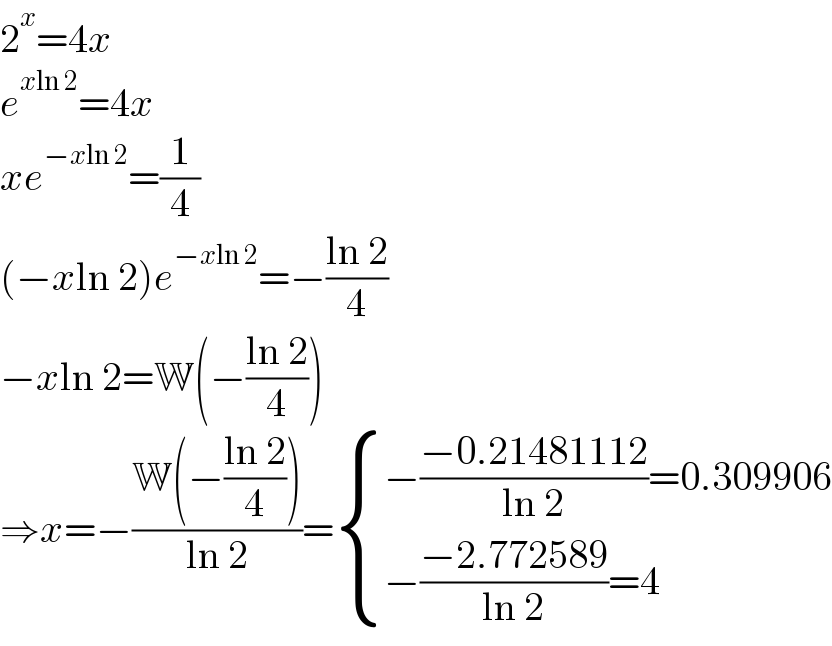
$$\mathrm{2}^{{x}} =\mathrm{4}{x} \\ $$$${e}^{{x}\mathrm{ln}\:\mathrm{2}} =\mathrm{4}{x} \\ $$$${xe}^{−{x}\mathrm{ln}\:\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\left(−{x}\mathrm{ln}\:\mathrm{2}\right){e}^{−{x}\mathrm{ln}\:\mathrm{2}} =−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}} \\ $$$$−{x}\mathrm{ln}\:\mathrm{2}=\mathbb{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}}\right) \\ $$$$\Rightarrow{x}=−\frac{\mathbb{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}}\right)}{\mathrm{ln}\:\mathrm{2}}=\begin{cases}{−\frac{−\mathrm{0}.\mathrm{21481112}}{\mathrm{ln}\:\mathrm{2}}=\mathrm{0}.\mathrm{309906}}\\{−\frac{−\mathrm{2}.\mathrm{772589}}{\mathrm{ln}\:\mathrm{2}}=\mathrm{4}}\end{cases} \\ $$
