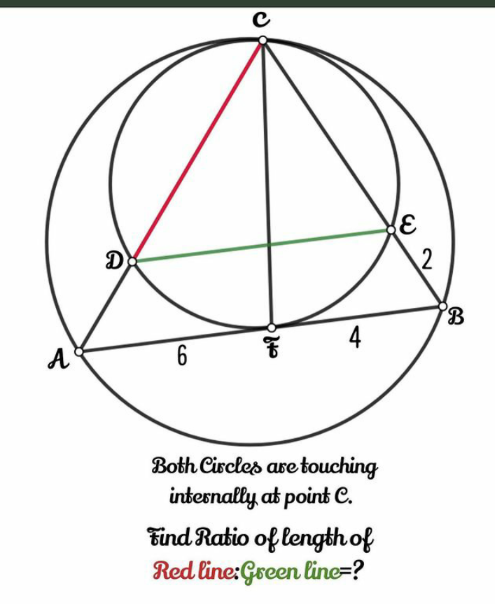
Question Number 139649 by mnjuly1970 last updated on 30/Apr/21
Commented by mr W last updated on 30/Apr/21

$$\frac{{red}}{{green}}=\frac{\mathrm{6}}{\mathrm{5}} \\ $$
Answered by mr W last updated on 30/Apr/21
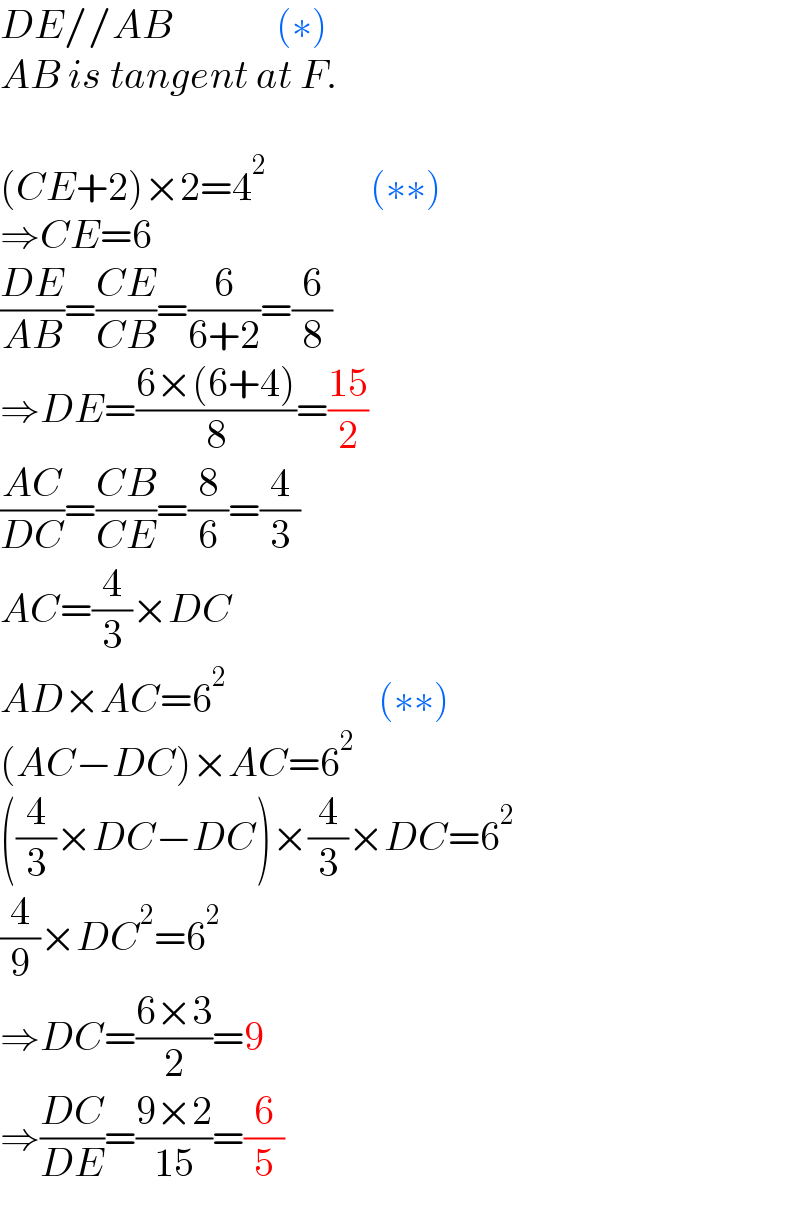
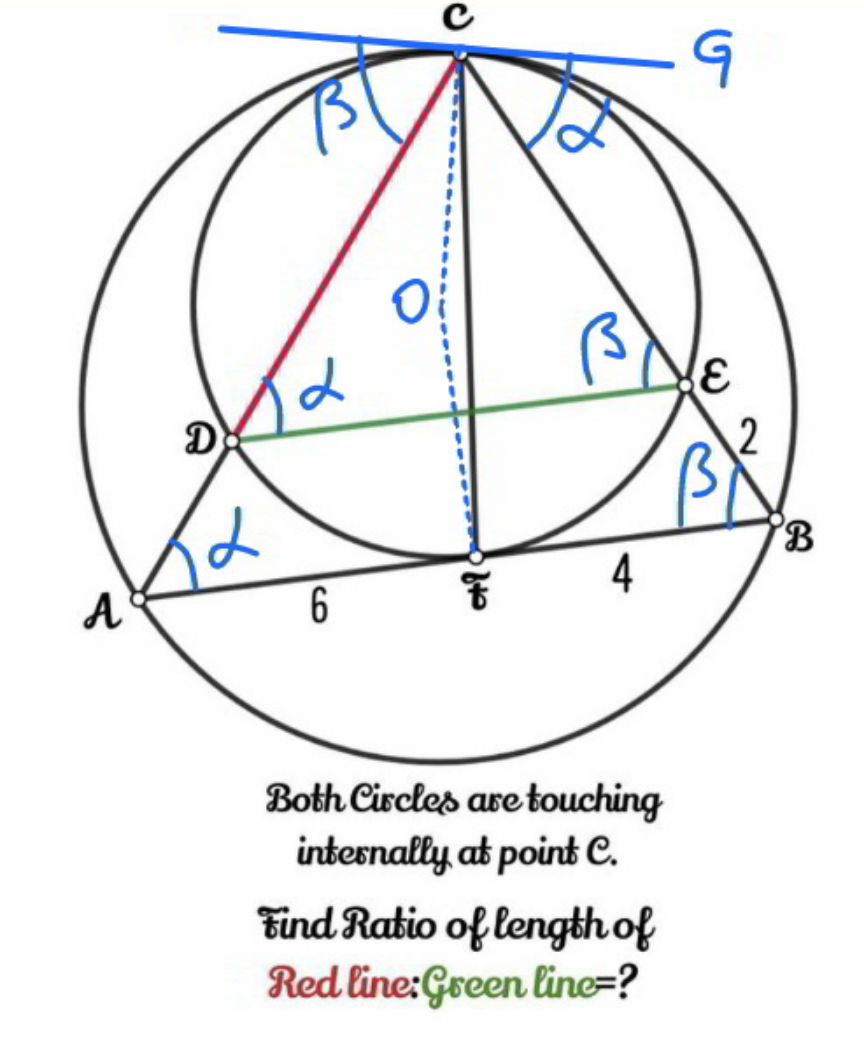
$${DE}//{AB}\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\ast\right) \\ $$$${AB}\:{is}\:{tangent}\:{at}\:{F}. \\ $$$$ \\ $$$$\left({CE}+\mathrm{2}\right)×\mathrm{2}=\mathrm{4}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\left(\ast\ast\right) \\ $$$$\Rightarrow{CE}=\mathrm{6} \\ $$$$\frac{{DE}}{{AB}}=\frac{{CE}}{{CB}}=\frac{\mathrm{6}}{\mathrm{6}+\mathrm{2}}=\frac{\mathrm{6}}{\mathrm{8}} \\ $$$$\Rightarrow{DE}=\frac{\mathrm{6}×\left(\mathrm{6}+\mathrm{4}\right)}{\mathrm{8}}=\frac{\mathrm{15}}{\mathrm{2}} \\ $$$$\frac{{AC}}{{DC}}=\frac{{CB}}{{CE}}=\frac{\mathrm{8}}{\mathrm{6}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${AC}=\frac{\mathrm{4}}{\mathrm{3}}×{DC} \\ $$$${AD}×{AC}=\mathrm{6}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\ast\ast\right) \\ $$$$\left({AC}−{DC}\right)×{AC}=\mathrm{6}^{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{4}}{\mathrm{3}}×{DC}−{DC}\right)×\frac{\mathrm{4}}{\mathrm{3}}×{DC}=\mathrm{6}^{\mathrm{2}} \\ $$$$\frac{\mathrm{4}}{\mathrm{9}}×{DC}^{\mathrm{2}} =\mathrm{6}^{\mathrm{2}} \\ $$$$\Rightarrow{DC}=\frac{\mathrm{6}×\mathrm{3}}{\mathrm{2}}=\mathrm{9} \\ $$$$\Rightarrow\frac{{DC}}{{DE}}=\frac{\mathrm{9}×\mathrm{2}}{\mathrm{15}}=\frac{\mathrm{6}}{\mathrm{5}} \\ $$
Commented by mr W last updated on 30/Apr/21
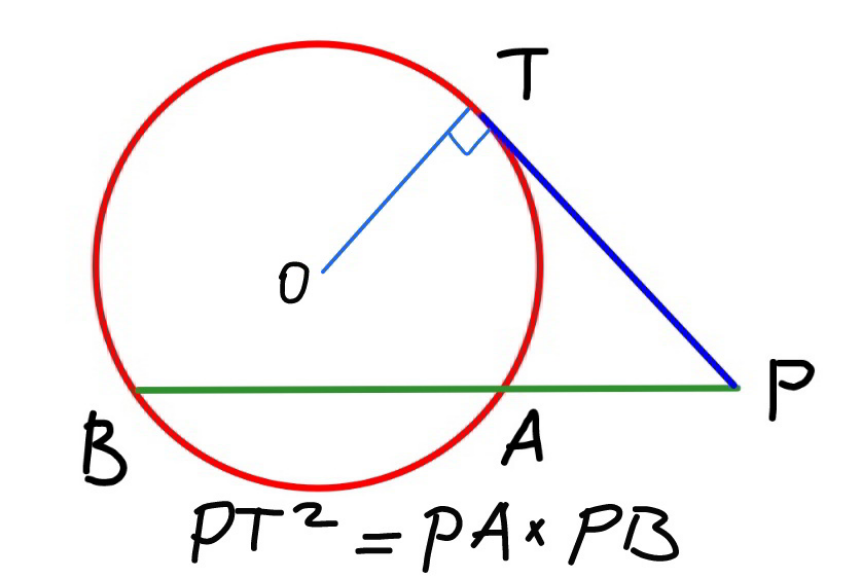
Commented by mnjuly1970 last updated on 30/Apr/21
$${very}\:{nice}\:{thanks}\:{alot}\:{mr}\:{W}.. \\ $$$${grateful}.. \\ $$
Commented by mr W last updated on 30/Apr/21
Commented by mr W last updated on 30/Apr/21
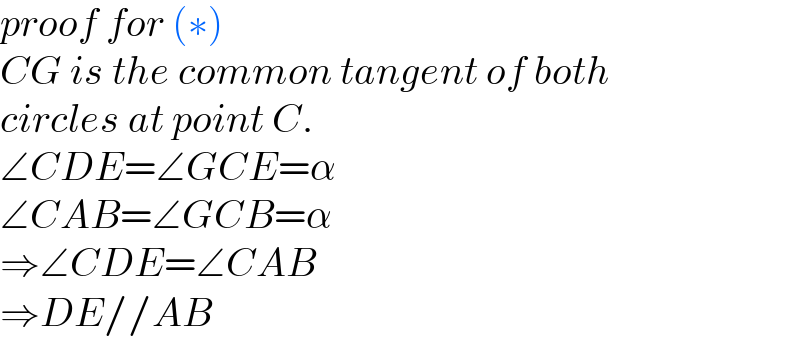
$${proof}\:{for}\:\left(\ast\right) \\ $$$${CG}\:{is}\:{the}\:{common}\:{tangent}\:{of}\:{both} \\ $$$${circles}\:{at}\:{point}\:{C}. \\ $$$$\angle{CDE}=\angle{GCE}=\alpha \\ $$$$\angle{CAB}=\angle{GCB}=\alpha \\ $$$$\Rightarrow\angle{CDE}=\angle{CAB} \\ $$$$\Rightarrow{DE}//{AB} \\ $$
Commented by mr W last updated on 30/Apr/21

$${proof}\:{for}\:\left(\ast\ast\right) \\ $$$${see}\:{Q}\mathrm{137946} \\ $$
Commented by mnjuly1970 last updated on 30/Apr/21

$${thanks}\:\:{alot}… \\ $$
