Question Number 139668 by aupo14 last updated on 30/Apr/21
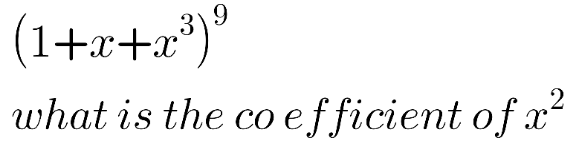
Commented by mr W last updated on 30/Apr/21
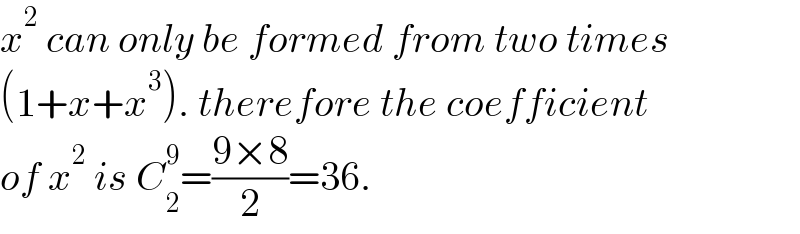
$${x}^{\mathrm{2}} \:{can}\:{only}\:{be}\:{formed}\:{from}\:{two}\:{times}\: \\ $$$$\left(\mathrm{1}+{x}+{x}^{\mathrm{3}} \right).\:{therefore}\:{the}\:{coefficient} \\ $$$${of}\:{x}^{\mathrm{2}} \:{is}\:{C}_{\mathrm{2}} ^{\mathrm{9}} =\frac{\mathrm{9}×\mathrm{8}}{\mathrm{2}}=\mathrm{36}. \\ $$
Commented by aupo14 last updated on 30/Apr/21
can you show me how x^2 will be formed just
two times? please?
Commented by mr W last updated on 01/May/21
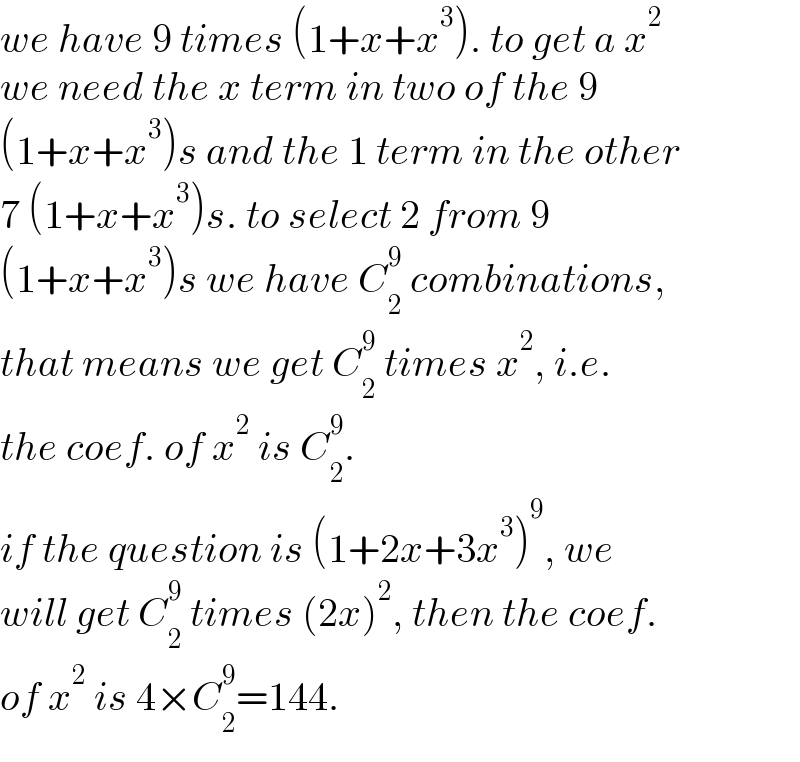
$${we}\:{have}\:\mathrm{9}\:{times}\:\left(\mathrm{1}+{x}+{x}^{\mathrm{3}} \right).\:{to}\:{get}\:{a}\:{x}^{\mathrm{2}} \\ $$$${we}\:{need}\:{the}\:{x}\:{term}\:{in}\:{two}\:{of}\:{the}\:\mathrm{9} \\ $$$$\left(\mathrm{1}+{x}+{x}^{\mathrm{3}} \right){s}\:{and}\:{the}\:\mathrm{1}\:{term}\:{in}\:{the}\:{other} \\ $$$$\mathrm{7}\:\left(\mathrm{1}+{x}+{x}^{\mathrm{3}} \right){s}.\:{to}\:{select}\:\mathrm{2}\:{from}\:\mathrm{9} \\ $$$$\left(\mathrm{1}+{x}+{x}^{\mathrm{3}} \right){s}\:{we}\:{have}\:{C}_{\mathrm{2}} ^{\mathrm{9}} \:{combinations}, \\ $$$${that}\:{means}\:{we}\:{get}\:{C}_{\mathrm{2}} ^{\mathrm{9}} \:{times}\:{x}^{\mathrm{2}} ,\:{i}.{e}. \\ $$$${the}\:{coef}.\:{of}\:{x}^{\mathrm{2}} \:{is}\:{C}_{\mathrm{2}} ^{\mathrm{9}} . \\ $$$${if}\:{the}\:{question}\:{is}\:\left(\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{3}} \right)^{\mathrm{9}} ,\:{we} \\ $$$${will}\:{get}\:{C}_{\mathrm{2}} ^{\mathrm{9}} \:{times}\:\left(\mathrm{2}{x}\right)^{\mathrm{2}} ,\:{then}\:{the}\:{coef}. \\ $$$${of}\:{x}^{\mathrm{2}} \:{is}\:\mathrm{4}×{C}_{\mathrm{2}} ^{\mathrm{9}} =\mathrm{144}. \\ $$
Answered by mr W last updated on 01/May/21
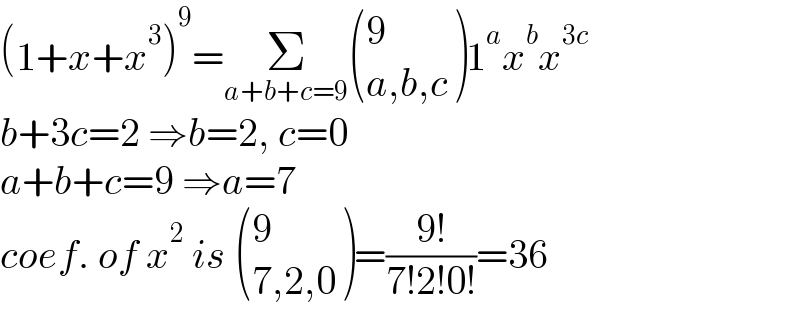
$$\left(\mathrm{1}+{x}+{x}^{\mathrm{3}} \right)^{\mathrm{9}} =\underset{{a}+{b}+{c}=\mathrm{9}} {\sum}\begin{pmatrix}{\mathrm{9}}\\{{a},{b},{c}}\end{pmatrix}\mathrm{1}^{{a}} {x}^{{b}} {x}^{\mathrm{3}{c}} \\ $$$${b}+\mathrm{3}{c}=\mathrm{2}\:\Rightarrow{b}=\mathrm{2},\:{c}=\mathrm{0} \\ $$$${a}+{b}+{c}=\mathrm{9}\:\Rightarrow{a}=\mathrm{7} \\ $$$${coef}.\:{of}\:{x}^{\mathrm{2}} \:{is}\:\begin{pmatrix}{\mathrm{9}}\\{\mathrm{7},\mathrm{2},\mathrm{0}}\end{pmatrix}=\frac{\mathrm{9}!}{\mathrm{7}!\mathrm{2}!\mathrm{0}!}=\mathrm{36} \\ $$
