Question Number 139696 by mnjuly1970 last updated on 30/Apr/21
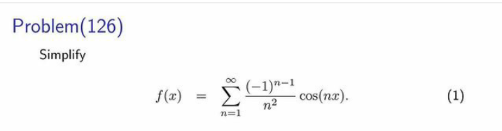
Answered by Dwaipayan Shikari last updated on 30/Apr/21
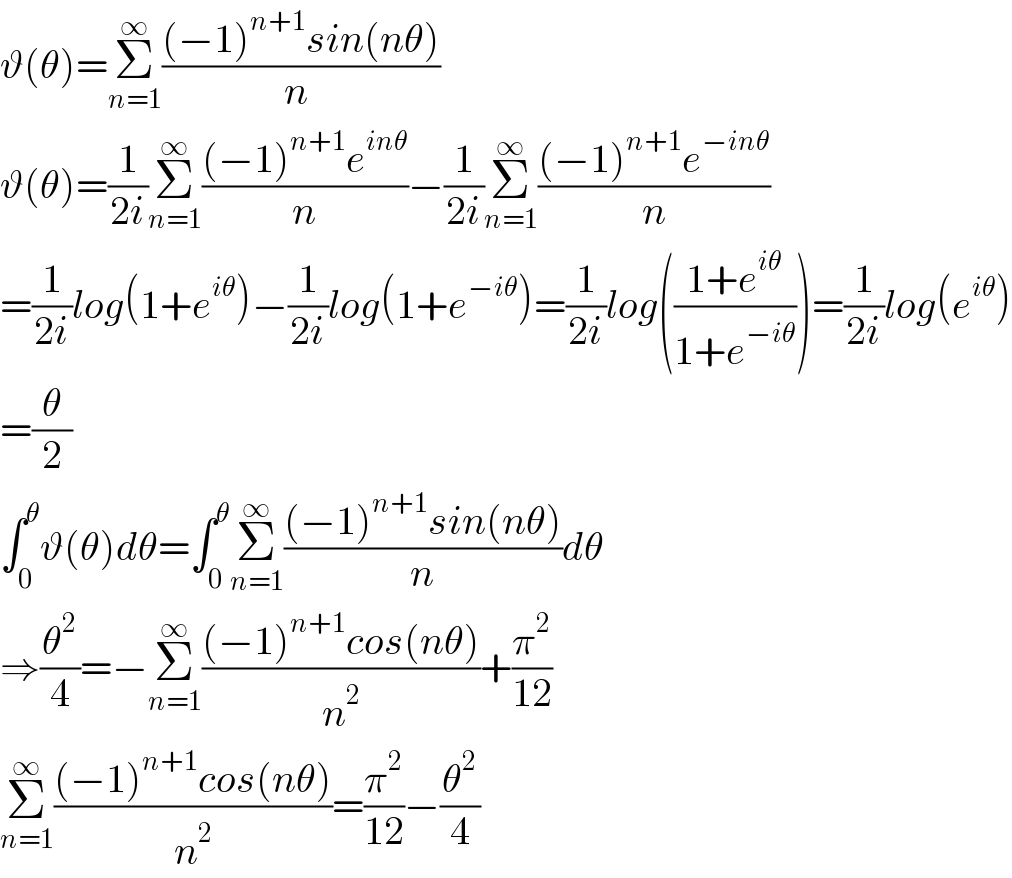
$$\vartheta\left(\theta\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {sin}\left({n}\theta\right)}{{n}\:} \\ $$$$\vartheta\left(\theta\right)=\frac{\mathrm{1}}{\mathrm{2}{i}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {e}^{{in}\theta} }{{n}}−\frac{\mathrm{1}}{\mathrm{2}{i}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {e}^{−{in}\theta} }{{n}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}{log}\left(\mathrm{1}+{e}^{{i}\theta} \right)−\frac{\mathrm{1}}{\mathrm{2}{i}}{log}\left(\mathrm{1}+{e}^{−{i}\theta} \right)=\frac{\mathrm{1}}{\mathrm{2}{i}}{log}\left(\frac{\mathrm{1}+{e}^{{i}\theta} }{\mathrm{1}+{e}^{−{i}\theta} }\right)=\frac{\mathrm{1}}{\mathrm{2}{i}}{log}\left({e}^{{i}\theta} \right) \\ $$$$=\frac{\theta}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\theta} \vartheta\left(\theta\right){d}\theta=\int_{\mathrm{0}} ^{\theta} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {sin}\left({n}\theta\right)}{{n}}{d}\theta \\ $$$$\Rightarrow\frac{\theta^{\mathrm{2}} }{\mathrm{4}}=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {cos}\left({n}\theta\right)}{{n}^{\mathrm{2}} }+\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {cos}\left({n}\theta\right)}{{n}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\frac{\theta^{\mathrm{2}} }{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 30/Apr/21

$${thanks}\:{alot}\:{mr}\:{payan}… \\ $$
