Question-139842

Question Number 139842 by I want to learn more last updated on 01/May/21

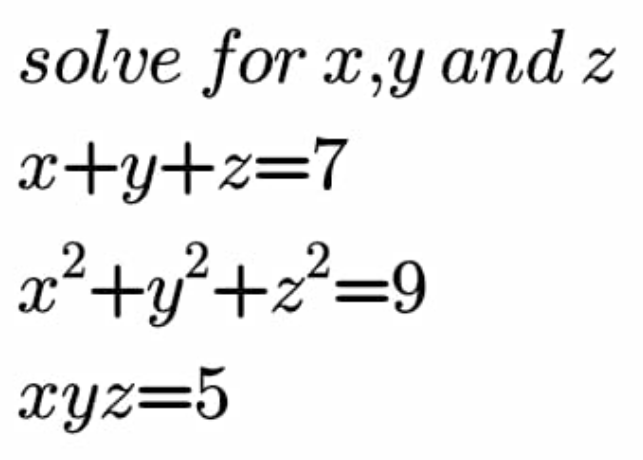
Commented by MJS_new last updated on 01/May/21

$$\mathrm{no}\:\mathrm{real}\:\mathrm{solution} \\ $$

Answered by mr W last updated on 01/May/21

(x+y+z)^2 =x^2 +y^2 +z^2 +2(xy+yz+zx) ⇒xy+yz+zx=((7^2 −9)/2)=20 x+y+z=7 xyz=5 ⇒x,y,z are roots of following eqn.: t^3 −7t^2 +20t−5=0 let t=s+(7/3) ⇒s^3 +((11)/3)s+((439)/(27))=0 (√Δ)=(√((((11)/9))^3 +(((439)/(54)))^2 ))=((√(2445))/6) s_1 =((((√(2445))/6)−((439)/(54))))^(1/3) −((((√(2445))/6)+((439)/(54))))^(1/3) ⇒t_1 =(7/3)+((((√(2445))/6)−((439)/(54))))^(1/3) −((((√(2445))/6)+((439)/(54))))^(1/3) ≈0.275524 s_(2,3) =(1/2)(((((√(2445))/6)+((439)/(54))))^(1/3) −((((√(2445))/6)−((439)/(54))))^(1/3) )±((√3)/2)(((((√(2445))/6)+((439)/(54))))^(1/3) +((((√(2445))/6)−((439)/(54))))^(1/3) )i ⇒t_(2,3) =(7/3)+(1/2)(((((√(2445))/6)+((439)/(54))))^(1/3) −((((√(2445))/6)−((439)/(54))))^(1/3) )±((√3)/2)(((((√(2445))/6)+((439)/(54))))^(1/3) +((((√(2445))/6)−((439)/(54))))^(1/3) )i ≈3.362238±2.615837i (x,y,z)∈(t_1 ,t_2 ,t_3 )

$$\left({x}+{y}+{z}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} +\mathrm{2}\left({xy}+{yz}+{zx}\right) \\ $$$$\Rightarrow{xy}+{yz}+{zx}=\frac{\mathrm{7}^{\mathrm{2}} −\mathrm{9}}{\mathrm{2}}=\mathrm{20} \\ $$$${x}+{y}+{z}=\mathrm{7} \\ $$$${xyz}=\mathrm{5} \\ $$$$\Rightarrow{x},{y},{z}\:{are}\:{roots}\:{of}\:{following}\:{eqn}.: \\ $$$${t}^{\mathrm{3}} −\mathrm{7}{t}^{\mathrm{2}} +\mathrm{20}{t}−\mathrm{5}=\mathrm{0} \\ $$$${let}\:{t}={s}+\frac{\mathrm{7}}{\mathrm{3}} \\ $$$$\Rightarrow{s}^{\mathrm{3}} +\frac{\mathrm{11}}{\mathrm{3}}{s}+\frac{\mathrm{439}}{\mathrm{27}}=\mathrm{0} \\ $$$$\sqrt{\Delta}=\sqrt{\left(\frac{\mathrm{11}}{\mathrm{9}}\right)^{\mathrm{3}} +\left(\frac{\mathrm{439}}{\mathrm{54}}\right)^{\mathrm{2}} }=\frac{\sqrt{\mathrm{2445}}}{\mathrm{6}} \\ $$$${s}_{\mathrm{1}} =\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{2445}}}{\mathrm{6}}−\frac{\mathrm{439}}{\mathrm{54}}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{2445}}}{\mathrm{6}}+\frac{\mathrm{439}}{\mathrm{54}}} \\ $$$$\Rightarrow{t}_{\mathrm{1}} =\frac{\mathrm{7}}{\mathrm{3}}+\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{2445}}}{\mathrm{6}}−\frac{\mathrm{439}}{\mathrm{54}}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{2445}}}{\mathrm{6}}+\frac{\mathrm{439}}{\mathrm{54}}} \\ $$$$\:\:\:\:\:\:\:\:\:\approx\mathrm{0}.\mathrm{275524} \\ $$$${s}_{\mathrm{2},\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{2445}}}{\mathrm{6}}+\frac{\mathrm{439}}{\mathrm{54}}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{2445}}}{\mathrm{6}}−\frac{\mathrm{439}}{\mathrm{54}}}\right)\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{2445}}}{\mathrm{6}}+\frac{\mathrm{439}}{\mathrm{54}}}+\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{2445}}}{\mathrm{6}}−\frac{\mathrm{439}}{\mathrm{54}}}\right){i} \\ $$$$\Rightarrow{t}_{\mathrm{2},\mathrm{3}} =\frac{\mathrm{7}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{2445}}}{\mathrm{6}}+\frac{\mathrm{439}}{\mathrm{54}}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{2445}}}{\mathrm{6}}−\frac{\mathrm{439}}{\mathrm{54}}}\right)\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{2445}}}{\mathrm{6}}+\frac{\mathrm{439}}{\mathrm{54}}}+\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{2445}}}{\mathrm{6}}−\frac{\mathrm{439}}{\mathrm{54}}}\right){i} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\approx\mathrm{3}.\mathrm{362238}\pm\mathrm{2}.\mathrm{615837}{i} \\ $$$$ \\ $$$$\left({x},{y},{z}\right)\in\left({t}_{\mathrm{1}} ,{t}_{\mathrm{2}} ,{t}_{\mathrm{3}} \right) \\ $$

Commented by I want to learn more last updated on 01/May/21

$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Commented by I want to learn more last updated on 01/May/21

Question sir. What is the formular to compute the values of t sir. Both real and complex.

$$\mathrm{Question}\:\mathrm{sir}. \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{formular}\:\mathrm{to}\:\mathrm{compute}\:\mathrm{the}\:\mathrm{values}\:\mathrm{of}\:\mathrm{t}\:\mathrm{sir}.\:\:\mathrm{Both}\:\mathrm{real}\:\mathrm{and}\:\mathrm{complex}. \\ $$

Commented by mr W last updated on 02/May/21